题目内容
15.计算:$\frac{1}{a-b}-\frac{a}{{a}^{2}-{b}^{2}}$=$\frac{b}{{a}^{2}-{b}^{2}}$.分析 原式通分并利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:原式=$\frac{a+b}{(a+b)(a-b)}$-$\frac{a}{(a+b)(a-b)}$
=$\frac{a+b-a}{(a+b)(a-b)}$
=$\frac{b}{{a}^{2}-{b}^{2}}$.
故答案为:$\frac{b}{{a}^{2}-{b}^{2}}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列运算正确的是( )
| A. | a2+a3=a5 | B. | 2a-a=2 | C. | a6÷a3=a2 | D. | (a2)3=a6 |
5.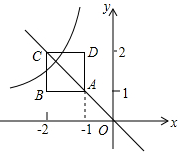 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )| A. | -4≤k≤-1 | B. | -4<k<-1 | C. | -4≤k<-1 | D. | 1≤k≤4 |
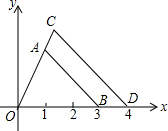 已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).
已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).