题目内容
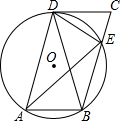
 如图,AB为⊙O的直径,CD为弦,AB=10,CD=6,且CD∥AB,则S四边形ABCD=
如图,AB为⊙O的直径,CD为弦,AB=10,CD=6,且CD∥AB,则S四边形ABCD=考点:垂径定理,勾股定理
专题:计算题
分析:作OE⊥DC,连结OC,根据垂径定理由OE⊥DC得CE=
DC=3,在Rt△OCE中,利用勾股定理可计算出OE=4,然后根据梯形的面积公式计算即可.
| 1 |
| 2 |
解答: 解:作OE⊥DC,连结OC,如图,
解:作OE⊥DC,连结OC,如图,
∵OE⊥DC,
∴CE=DE=
DC=
×6=3,
∵直径AB=10,
∴OC=5,
在Rt△OCE中,OE=
=4,
∴S四边形ABCD=
×(6+10)×4=32.
故答案为32.
 解:作OE⊥DC,连结OC,如图,
解:作OE⊥DC,连结OC,如图,∵OE⊥DC,
∴CE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
∵直径AB=10,
∴OC=5,
在Rt△OCE中,OE=
| OC2-CE2 |
∴S四边形ABCD=
| 1 |
| 2 |
故答案为32.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE. 在平行四边形ABCD中,M1是边AD的中点,N1是边BC的中点,从A,B,C,D,M1,N1中选取四个点构造平行四边形,则能构造
在平行四边形ABCD中,M1是边AD的中点,N1是边BC的中点,从A,B,C,D,M1,N1中选取四个点构造平行四边形,则能构造 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF,若OG=2,则EF为
如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF,若OG=2,则EF为