题目内容
12.已知点P(a,b)在直线y=$\frac{1}{2}$x-1上,点Q(-a,2b)在直线y=x+1上,则代数式a2-4b2-1的值为1.分析 将点的坐标代入直线中可得出关于a、b的二元一次方程组,解方程即可得出a、b的值,将其代入代数式a2-4b2-1中,即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{b=\frac{1}{2}a-1}\\{2b=-a+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-\frac{1}{4}}\end{array}\right.$.
∴a2-4b2-1=$(\frac{3}{2})^{2}$-4×$(-\frac{1}{4})^{2}$-1=1.
故答案为:1.
点评 本题考查了一次函数图象上点的坐标特征以及解二元一次方程组,解题的关键是求出a、b的值.本题属于基础题,难度不大,解决该题型题目时,由点在直线上得出方程(或方程组)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.国家气象局监测2015年某日24小时PM2.5的值,其中6个时刻的数值如表:
则这组数据的中位数和平均数分别是( )
| 时刻 | 4时 | 5时 | 6时 | 7时 | 8时 | 9时 |
| PM2.5(毫克∕立方米) | 342 | 342 | 333 | 329 | 325 | 324 |
| A. | 331;332.5 | B. | 329;332.5 | C. | 331;332 | D. | 333;332 |
16.化简$\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2+\sqrt{3}}}$的结果是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
 如图,点P在△ABC的边AC上,请你添加一个条件,使得△ABP∽△ACB,这个条件可以是∠ABP=∠C(答案不唯一).
如图,点P在△ABC的边AC上,请你添加一个条件,使得△ABP∽△ACB,这个条件可以是∠ABP=∠C(答案不唯一).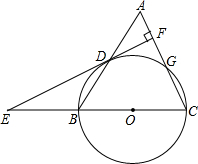 如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.
如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.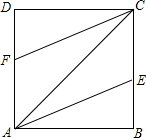 如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F. 如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.
如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.