题目内容
19.已知x=$\root{2m-3n}{m+n+3}$是m+n+3的算术平方根,y=$\root{m-n+1}{m+2n}$是m+2n的立方根,求(x-y)2007的平方根.分析 由算术平方根和立方根的定义可知2m-3n=2,m-n+1=3,从而可求得m、n的值,进而可得到x、y的值,最后再求得(x-y)2007的平方根即可.
解答 解:∵x=$\root{2m-3n}{m+n+3}$是m+n+3的算术平方根,y=$\root{m-n+1}{m+2n}$是m+2n的立方根,
∴2m-3n=2,m-n+1=3.
解得:m=4,n=2.
∴x=3,y=2.
∴(x-y)2007=(3-2)2007=1.
∴(x-y)2007的平方根是±1.
点评 本题主要考查的是平方根、算术平方根、立方根的定义,求得x、y的值是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 .
.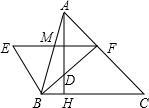 如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )
如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )