题目内容
14.化简:(1)$\frac{-6{m}^{2}n}{24m{n}^{2}}$=-$\frac{m}{4n}$;(2)$\frac{(a-b)(b-c)(c-a)}{(a-c)(c-b)(b-a)}$=-1.分析 (1)根据分式的基本性质,约去分子与分母的公因式6mn即可;
(2)先将原式变形为$\frac{(a-b)(b-c)(c-a)}{[-(c-a)][-(b-c)][-(a-b)]}$=$\frac{(a-b)(b-c)(c-a)}{-(a-b)(b-c)(c-a)}$,再根据分式的基本性质,约去分子与分母的公因式(a-b)(b-c)(c-a)即可.
解答 解:(1)$\frac{-6{m}^{2}n}{24m{n}^{2}}$=-$\frac{m}{4n}$;
(2)$\frac{(a-b)(b-c)(c-a)}{(a-c)(c-b)(b-a)}$=$\frac{(a-b)(b-c)(c-a)}{[-(c-a)][-(b-c)][-(a-b)]}$=$\frac{(a-b)(b-c)(c-a)}{-(a-b)(b-c)(c-a)}$=-1.
故答案为-$\frac{m}{4n}$;-1.
点评 本题考查了约分,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.注意:分式约分的结果可能是最简分式,也可能是整式.当分子与分母含有负号时,一般把负号提到分式本身的前面.

练习册系列答案
相关题目
5.$\sqrt{(-4)^{2}}$的平方根与$\sqrt{(-2)^{2}}$的和的绝对值是( )
| A. | 0 | B. | 4 | C. | 0或2 | D. | 4或0 |
2.若一元二次方程3x2-mx+8=0的一个根为2,则m的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 无法确定 |
9.若A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x-6的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
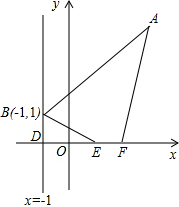 已知点A(3,4),点B(-1,1),在x轴上另取两点E,F(点E在点F的左侧),且EF=1,线段EF在x上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.
已知点A(3,4),点B(-1,1),在x轴上另取两点E,F(点E在点F的左侧),且EF=1,线段EF在x上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标.
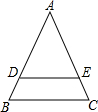 如图,在△ABC中,已知DE∥BC,AE=3EC,S△ABC=48,求S△ADE及S四边形BCED.
如图,在△ABC中,已知DE∥BC,AE=3EC,S△ABC=48,求S△ADE及S四边形BCED.