题目内容
17. 如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=4,BC=3,求DG的长.
如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=4,BC=3,求DG的长.
分析 首先由折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,即可得:∠GDA=∠GDB,AD=ED,然后过点G作GE⊥BD于E,即可得AG=EG,设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,在Rt△BEG中利用勾股定理,即可求得AG的长,然后根据勾股定理即可得到结论.
解答 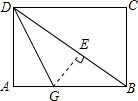 解:过点G作GE⊥BD于E,
解:过点G作GE⊥BD于E,
根据题意可得:∠GDA=∠GDB,AD=ED,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3,
∴AG=EG,ED=3,
∵AB=4,BC=3,∠A=90°,
∴BD=5,
设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,
在Rt△BEG中,EG2+BE2=BG2,
即:x2+4=(4-x)2,
解得:x=$\frac{3}{2}$,
∴AG=$\frac{3}{2}$,
∴DG=$\sqrt{A{D}^{2}+A{G}^{2}}$=$\frac{3}{2}$$\sqrt{5}$.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理等知识.此题综合性很强,难度适中,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
相关题目
7.若抛物线y=x2-x-1与x轴的交点坐标为(m,0),则代数式m2-m+2012的值为( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
8.下列有理数大小关系判断正确的是( )
| A. | 0>|-10| | B. | -(-$\frac{1}{9}$)>-|-$\frac{1}{10}$| | C. | |-3|<|+3| | D. | -1>-0.01 |
6.y=$\frac{6}{x}$上有两点A(x1,y1)与B(x2,y2),若x1<x2,则y1与y2的关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
 如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.
如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.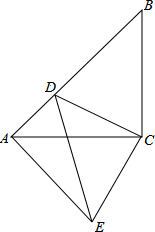 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.