题目内容
7.在平面直角坐标系中,已知点A(0,a),抛物线y=-a(x-a)2+b与x轴交于B、C两点(|OB|<|OC|),顶点为D,且AD∥BC,tan∠ABO=$\frac{3}{2}$,则满足条件的抛物线有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 根据点A(0,a),抛物线y=-a(x-a)2+b与x轴交于B、C两点(|OB|<|OC|),顶点为D,且AD∥BC,tan∠ABO=$\frac{3}{2}$,可以得到符合条件的抛物线有两种情况,从而可以解答本题.
解答 解:∵抛物线y=-a(x-a)2+b与x轴交于B、C两点(|OB|<|OC|),顶点为D,且AD∥BC,tan∠ABO=$\frac{3}{2}$,A(0,a),
∴该抛物线的对称轴x=a,
当a>0时,该抛物线开口向下,点A在y轴的正半轴,抛物线的顶点在第一象限,点B、点C在x轴的正半轴,且|OB|<|OC|,
当a<0时,该抛物线开口向上,点A在y轴的负半轴,抛物线的顶点在第三象限,点B、点C在x轴的负半轴,且|OB|<|OC|,
故满足条件的有两种情况,
故选B.
点评 本题考查抛物线与x轴的交点,解题的关键是明确题意,根据已知条件可以判断符合条件的抛物线有几种情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.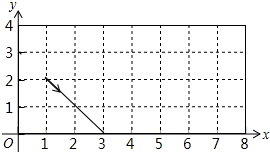 如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
 如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )| A. | (0,5) | B. | (5,0) | C. | (3,3) | D. | (7,3) |
 如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=4,BC=3,求DG的长.
如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=4,BC=3,求DG的长. 如图,平面展开图折叠成正方体后,相对面上的两个代数式值相等,则x+y=5.
如图,平面展开图折叠成正方体后,相对面上的两个代数式值相等,则x+y=5. 某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工,如图的线段和折线是两对前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象.
某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工,如图的线段和折线是两对前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象.