题目内容
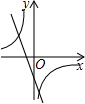
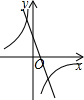
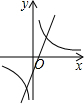
15.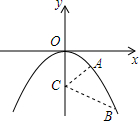 如图所示,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,使AC+BC距离最短,求C点的坐标.
如图所示,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,使AC+BC距离最短,求C点的坐标.
分析 找出点A关于y轴的对称点A′,连接A′B与y轴相交于点C,根据轴对称确定最短路线问题,点C即为使AC+BC最短的点,再根据抛物线解析式求出点A′、B的坐标,然后利用勾股定理列式计算即可得解.
解答 解:找出点A关于y轴的对称点A′,连接A′B与y轴相交于点C,
根据轴对称确定最短路线问题,点C即为使AC+BC最短的点,
根据抛物线解析式求出点A′、B的坐标,
A为(-1,-1),B为(-2,-4),
设直线A′B为y=kx+b,则$\left\{\begin{array}{l}{-1=-k+b}\\{-4=2k+b}\end{array}\right.$,
解得k=-1,b=-2.
所以y=-x-2,
所以C(0,-2).
点评 本题考查了轴对称确定最短路线问题,二次函数的性质,熟记确定出最短路径的方法和二次函数的对称性确定出点C的位置是解题的关键.

练习册系列答案
相关题目
5. 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )| A. | ∠F | B. | ∠FDE | C. | ∠E | D. | 以上都不正确 |
6.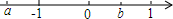 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
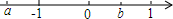 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )| A. | -2a | B. | 2b | C. | -2b | D. | 2a |
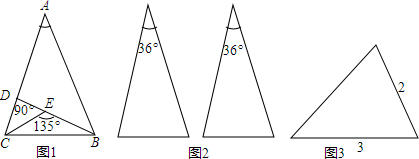
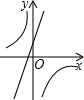
 如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.
如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.