题目内容
12.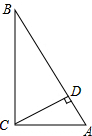 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若∠A=60°,AD=2cm,则AB=8cm.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若∠A=60°,AD=2cm,则AB=8cm.
分析 根据同角的余角相等求出∠ACD=∠B=30°,再根据30°角所对的直角边等于斜边的一半求出AC,再求出AB的长即可得解.
解答 解:∵∠ACB=90°,CD⊥AB,
∴∠B+∠A=90°,∠A+∠ACD=90°,
∴∠ACD=∠B=90°-∠A=30°,
∵AD=2cm,
∴AC=2AD=4cm,
∴AB=2AC=8cm,
故答案为:8cm.
点评 本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
3.下列变形错误的是( )
| A. | 如果x+7=26,那么x+5=24 | B. | 如果3x+2y=2x-y,那么3x+3y=2x | ||
| C. | 如果2a=5b,那么2ac=5bc | D. | 如果3x=4y,那么$\frac{3x}{{a}^{2}}$=$\frac{4y}{{a}^{2}}$ |
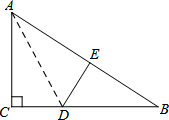 如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )
如图,折叠Rt△ABC,使直角边AC落在斜边AB上,点C落到点E处,已知AC=6cm,BC=8cm,则CD的长为( )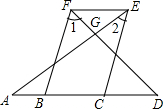 如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.
如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.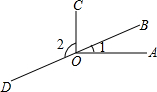 如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.
如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.