题目内容
7.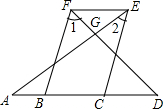 如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.
如图,A、B、C、D四点在同一条直线上,∠AGD=90°,且∠1=∠D,∠2=∠A.求证:FB∥EC.
分析 先由∠AGD=90°,根据三角形内角和定理得出∠A+∠D=90°,再由∠1=∠D,∠ABF=∠1+∠D,得出∠ABF=2∠D,同理得出∠DCE=2∠A,那么∠DCE+∠ABF=2(∠A+∠D)=180°,根据邻补角定义得出∠ABF+∠DBF=180°,由同角的补角相等得到∠DCE=∠DBF,根据同位角相等,两直线平行得出FB∥EC.
解答  证明:∵∠AGD=90°,
证明:∵∠AGD=90°,
∴∠A+∠D=90°,
∵∠1=∠D,∠ABF=∠1+∠D,
∴∠ABF=2∠D,
同理:∠DCE=2∠A,
∴∠DCE+∠ABF=2(∠A+∠D)=180°,
又∵∠ABF+∠DBF=180°,
∴∠DCE=∠DBF,
∴FB∥EC.
点评 本题考查了平行线的判定,三角形内角和定理,三角形外角的性质,邻补角定义,补角的性质,根据条件得出∠DCE=∠DBF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.点(-3,2)向下平移3个单位长度,再向右平移4个单位长度后位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.下列各式中是分式的是( )
| A. | x | B. | $\frac{x}{2}$ | C. | $\frac{2}{x}$ | D. | $\frac{1}{3}$ |
 如图,已知线段AB=6cm,BC=$\frac{1}{2}$AB,D是AC的中点,则BD=$\frac{3}{2}$cm.
如图,已知线段AB=6cm,BC=$\frac{1}{2}$AB,D是AC的中点,则BD=$\frac{3}{2}$cm.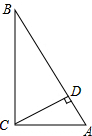 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若∠A=60°,AD=2cm,则AB=8cm.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若∠A=60°,AD=2cm,则AB=8cm.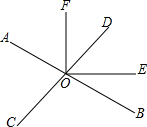 如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.
如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.