Question

10．如图，四边形ABCD是矩形，点E在CD边上，点F在DC延长线上，AE=BF．
（1）求证：四边形ABFE是平行四边形；
（2）若∠BEF=∠DAE，AE=3，BE=4，求EF的长．

Answer 1

分析 （1）欲证明四边形ABFE是平行四边形，只要证明AE∥BF，EF∥AB即可．
（2）先证明△AEB是直角三角形，再根据勾股定理计算即可．

解答 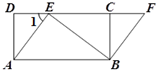（1）证明：∵四边形ABCD是矩形，
∴AD=BC，∠D=∠BCD=90°．
∴∠BCF=180°-∠BCD=180°-90°=90°．
∴∠D=∠BCF．在Rt△ADE和Rt△BCF中，
$\left\{\begin{array}{l}AE=BF\\ AD=BC.\end{array}\right.$
∴Rt△ADE≌Rt△BCF．
∴∠1=∠F．
∴AE∥BF．
∵AE=BF，
∴四边形ABFE是平行四边形．

（2）解：∵∠D=90°，
∴∠DAE+∠1=90°．
∵∠BEF=∠DAE，
∴∠BEF+∠1=90°．
∵∠BEF+∠1+∠AEB=180°，
∴∠AEB=90°．
在Rt△ABE中，AE=3，BE=4，
AB=$\sqrt{A{E^2}+B{E^2}}=\sqrt{{3^2}+{4^2}}=5$．
∵四边形ABFE是平行四边形，
∴EF=AB=5．

点评 本题考查矩形的性质、平行四边形的判定和性质、勾股定理，全等三角形的判定和性质等知识，解题的关键是熟练掌握这些知识的应用，属于中考基础题，常考题型．