题目内容
17.某超市试销一种成本为60元/件的夏季服装,规定试销期间销售单价不低于成本单价,且获利不得高于40%,经市场试销调研发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=80时,y=70;x=70时,y=80.(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,该超市的最大利润是多少元?(利润=销售收入-进货成本,不含其他支出)
分析 (1)直接利用待定系数法确定函数关系式进而得出答案;
(2)根据题意得出W与x之间的关系式,进而求出最大利润.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{80k+b=70}\\{70k+b=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=150}\end{array}\right.$,
所求一次函数的表达式为y=-x+150;
(2)W=(x-60)(-x+150)
=-x2+210x-9000
=-(x-105)2+2025
∵a=-1,
∴当x<105时,W随x的增大而增大,
又∵销售单价不低于成本单价,且获利不得高于40%,
∴60≤x≤60×(1+40%),即60≤x≤84,
∴当x=84时,W取得最大值为:-(84-105)2+2025=1584.
∴当销售单价定为84元时,商场可获得最大利润,最大利润是1584元.
点评 此题主要考查了二次函数的应用,正确得出二次函数关系式是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
5.我市某中学九(1)班为“阳光体育运动”自筹资金购买体育器材,全班40名同学筹款情况如下表,则该班同学筹款金额的众数是15元.
| 筹款金额(元) | 10 | 15 | 20 |
| 人数 | 10 | 17 | 13 |
2.计算:(-1)2017的值是( )
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
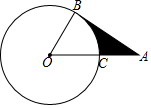 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π. 如图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式c2=a2+b2.
如图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等式c2=a2+b2. 如图,在△ABC中,∠C=90°,它的周长为(2+$\sqrt{6}$)cm,AB=2cm,求△ABC的面积.
如图,在△ABC中,∠C=90°,它的周长为(2+$\sqrt{6}$)cm,AB=2cm,求△ABC的面积.