题目内容
17.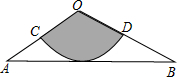 如图,从一张腰长为6cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥底面半径为1cm.
如图,从一张腰长为6cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥底面半径为1cm.
分析 根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长,设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到r即可.
解答  解:过O作OE⊥AB于E,∵OA=OB=6cm,∠AOB=120°,
解:过O作OE⊥AB于E,∵OA=OB=6cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=$\frac{1}{2}$OA=3cm,
∴弧CD的长=$\frac{120π×3}{180}$=2π,
设圆锥的底面圆的半径为r,
则2πr=2π,
解得r=1,
故答案为:1.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8.下列各有理式中,为分式的是( )
| A. | $\frac{x}{3x-1}$ | B. | -$\frac{{x}^{2}+1}{2}$ | C. | $\frac{\sqrt{5y}}{x}$ | D. | $\frac{(x+2)(x-2)}{π}$ |
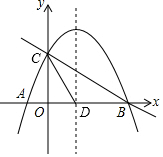 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.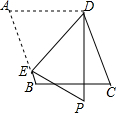 如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.
如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.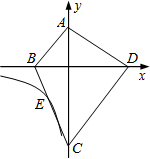 如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )