题目内容
13.有四张背面完全相同的不透明卡片,正面分别写着-3、-2、2、3,把这四张卡片正面朝下放在桌面上,从中任意抽取一张,将卡片上的数字记为m,再从剩下的卡片中任取一张,并把卡片上的数字记为n,则使得直线y=mx+n不经过第三象限的概率为$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所得到的直线y=mx+n不经过第三象限的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
由树状图或列表可知共有12种等可能的结果,其中图象直线y=mx+n不经过第三象限的情况有4种,分别是m=-3,n=2;m=-3,n=3;m=-2,n=2;m=-2,n=3;
故使得直线y=mx+n不经过第三象限的概率为$\frac{4}{12}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查的是用列表法或树状图法求概率与一次函数的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
4.关于x的一元二次方程x2-ax-1=0(其中a为常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 可能有实数根,也可能没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
1.已知点A的坐标是(a,b),若a+b<0,ab>0,则它在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.下列各有理式中,为分式的是( )
| A. | $\frac{x}{3x-1}$ | B. | -$\frac{{x}^{2}+1}{2}$ | C. | $\frac{\sqrt{5y}}{x}$ | D. | $\frac{(x+2)(x-2)}{π}$ |
18.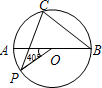 如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
 如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2=50度.
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2=50度.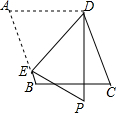 如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.
如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.