题目内容
15.在Rt△ABC中,∠A=90°,$\frac{AB}{BC}=\frac{1}{{\sqrt{3}}}$,那么cosC=$\frac{\sqrt{6}}{3}$.分析 由在Rt△ABC中,∠A=90°,$\frac{AB}{BC}=\frac{1}{{\sqrt{3}}}$,设AB=k,可得BC=$\sqrt{3}$k,AC=$\sqrt{2}$k,即可求解cosC的值.
解答 解:如图,
∵在Rt△ABC中,∠A=90°,$\frac{AB}{BC}=\frac{1}{{\sqrt{3}}}$,
设AB=k,则BC=$\sqrt{3}$k,AC=$\sqrt{2}$k,
∴cosC=$\frac{AC}{BC}$=$\frac{\sqrt{2}k}{\sqrt{3}k}$=$\frac{\sqrt{6}}{3}$.
故答案为:$\frac{{\sqrt{6}}}{3}$.
点评 本题主要考查了锐角三角形函数的定义,解题的关键是确定三角形三边的长度.

练习册系列答案
相关题目
5.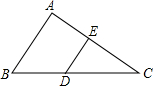 如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
 如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
10.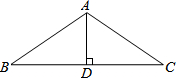 如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
①△ABD≌△ACD;②△ABD与△ACD不全等;③AB=AC;④∠B=∠C;⑤AD平分∠BAC.
其中正确的是( )
 如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:①△ABD≌△ACD;②△ABD与△ACD不全等;③AB=AC;④∠B=∠C;⑤AD平分∠BAC.
其中正确的是( )
| A. | ①③④ | B. | ②③④⑤ | C. | ①③④⑤ | D. | ③⑤ |
2.某县决定鼓励农民开荒种植花木并实行政府补贴,规定每新种植一亩花木一次性补贴农户若干元,经调查,种植亩数y(亩)与补贴金额x(元)之间成一次函数关系,且补贴与种植情况如下表:
随着补贴数额x的不断增大,种植规模也不断增加,但每亩花木的收益z(元)会相应降低,且该县补贴政策实施前每亩花木收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩花木的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数y(亩).每亩花木的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县新种植的花木总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,需占用其中不超过50亩的新种花木园,利用其树间空地种植新品种花木,已知引进该新品种平均每亩的费用为530元,此外还要购置其他设备,这一费用(元)等于种植面积(亩)的平方的25倍.这样混种了新品种花木的这部分土地比原来种植单一品种花木时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为80000元,求混种花木的土地有多少亩?
| 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
(1)分别求出政府补贴政策实施后,种植亩数y(亩).每亩花木的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县新种植的花木总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,需占用其中不超过50亩的新种花木园,利用其树间空地种植新品种花木,已知引进该新品种平均每亩的费用为530元,此外还要购置其他设备,这一费用(元)等于种植面积(亩)的平方的25倍.这样混种了新品种花木的这部分土地比原来种植单一品种花木时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为80000元,求混种花木的土地有多少亩?
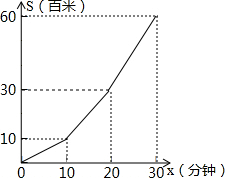 小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.
小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.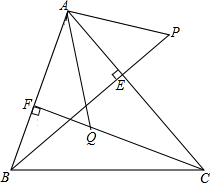 如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.