题目内容
19.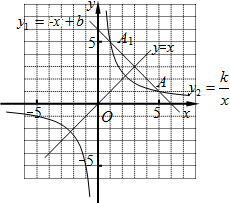 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )| A. | x≥5 | B. | 0<x≤-1 | C. | 1≤x≤5 | D. | x≥5或 0<x≤1 |
分析 抛物线关于直线y=x轴对称,可证直线y1=-x+6与直线y=x互相垂直,根据轴对称性可求点A1的坐标,再根据y1与y2的图象的位置关系,求x的取值范围.
解答 解:由函数图象根据题意可知A1(1,5),
当0<x≤1或x≥5时,y1≤y2.
所以不等式$\frac{k}{x}$+x-b≥0的解是0<x≤1或x≥5;
故选D.
点评 本题考查了反比例函数与一次函数的交点问题.关键是结合图象的位置根据对称性求得点A1的坐标.

练习册系列答案
相关题目
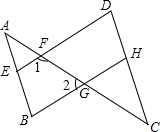 如图,已知:∠A=∠C,∠B=∠D.你能确定图中∠1与∠2的数量关系吗?请写出你的结论并进行证明.
如图,已知:∠A=∠C,∠B=∠D.你能确定图中∠1与∠2的数量关系吗?请写出你的结论并进行证明.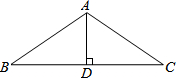 如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
如图,已知AD⊥BC,D是垂足,BD=CD,下列判断: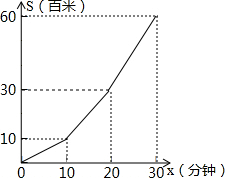 小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.
小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.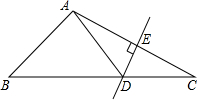 如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为19.
如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为19.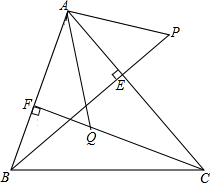 如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
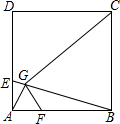 如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证:
如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证: