题目内容
 已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E
已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E (1)求证:△BCE∽△AGC;
(2)点P是射线AD上的一个动点,设AP=x,四边形ACEP的面积是y,若AF=5,AD=
| 25 |
| 3 |
①求y关于x的函数关系式,并写出定义域;
②当点P在射线AD上运动时,是否存在这样的点P,使得△CPE的周长为最小?若存在,求出此时y的值,若不存在,请说明理由.
考点:相似形综合题
专题:证明题
分析:(1)先利用等腰三角形的性质得到∠1=∠2,再利用等角的余角相等得到∠2=∠3,则∠1=∠3,然后利用AD∥EF得到∠BCE=∠AGC=90°,于是可判断△BCE∽△AGC;
(2)①先证明四边形ADEF为平行四边形得到DE=AF=5,再说明DG为△BCE的中位线得到DG=
CE,BD=DE=5,在Rt△ABD中根据勾股定理计算出AB=
,接着利用面积法计算出BG=4,则CG=4,再利用勾股定理易得DG=3,则CE=2DG=6,然后根据梯形得面积公式得到y与x的关系;
②由于△CPE的周长═PC+PE+6,再根据AD垂直平分BC得到PB=PC,所以△CPE的周长=PB+PE+6,由于PB+PE≥BE,则PB+PE=BE时,即点P与点D重合,△PCE的周长最小,求出此时的x的值,然后利用①中的关系求出对应的y的值.
(2)①先证明四边形ADEF为平行四边形得到DE=AF=5,再说明DG为△BCE的中位线得到DG=
| 1 |
| 2 |
| 20 |
| 3 |
②由于△CPE的周长═PC+PE+6,再根据AD垂直平分BC得到PB=PC,所以△CPE的周长=PB+PE+6,由于PB+PE≥BE,则PB+PE=BE时,即点P与点D重合,△PCE的周长最小,求出此时的x的值,然后利用①中的关系求出对应的y的值.
解答:(1)证明:如图,∵AB=AC,AG⊥BC,
∴∠1=∠2,BG=CG,∠AGC=90°,
∴∠2+∠AGB=90°,
而∠ABG+∠3=90°,
∴∠1=∠3,
∵AD∥EF,
∴∠BCE=∠AGC=90°,
∴△BCE∽△AGC;
(2)①解:∵AF∥DE,AD∥EF,
∴四边形ADEF为平行四边形,
∴DE=AF=5,
∵BG=CG,DG∥CE,
∴DG为△BCE的中位线,
∴DG=
CE,BD=DE=5,
在Rt△ABD中,∵AD=
,BD=5,
∴AB=
=
,
∵
BG•AD=
AB•BD,
∴BG=
=4,
∴CG=4,
在Rt△BDG中,∵BD=5,BG=4,
∴DG=
=3,
∴CE=2DG=6,
∴y=
(6+x)•4=2x+12(x>0);
②存在.
连结PB,PC,如图,
△CPE的周长=PC+PE+CE
=PC+PE+6,
∵AD垂直平分BC,
∴PB=PC,
∴△CPE的周长=PB+PE+6,
∵PB+PE≥BE,
∴当PB+PE=BE时,即点P与点D重合,△PCE的周长最小,
此时x=
,
∴y=2×
+12=
.
∴∠1=∠2,BG=CG,∠AGC=90°,
∴∠2+∠AGB=90°,
而∠ABG+∠3=90°,
∴∠1=∠3,
∵AD∥EF,
∴∠BCE=∠AGC=90°,
∴△BCE∽△AGC;
(2)①解:∵AF∥DE,AD∥EF,
∴四边形ADEF为平行四边形,
∴DE=AF=5,
∵BG=CG,DG∥CE,
∴DG为△BCE的中位线,
∴DG=
| 1 |
| 2 |
在Rt△ABD中,∵AD=
| 25 |
| 3 |
∴AB=
| AD2-BD2 |
| 20 |
| 3 |

∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BG=
| ||
|
∴CG=4,
在Rt△BDG中,∵BD=5,BG=4,
∴DG=
| BD2-BG2 |
∴CE=2DG=6,
∴y=
| 1 |
| 2 |
②存在.
连结PB,PC,如图,
△CPE的周长=PC+PE+CE
=PC+PE+6,
∵AD垂直平分BC,
∴PB=PC,
∴△CPE的周长=PB+PE+6,
∵PB+PE≥BE,
∴当PB+PE=BE时,即点P与点D重合,△PCE的周长最小,
此时x=
| 25 |
| 3 |
∴y=2×
| 25 |
| 3 |
| 86 |
| 3 |
点评:本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,也考查了等腰三角形的性质、平行四边形的判定与性质和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )
如图所示,已知OA=OB,OC=OD,AD、BC相交于点E,则图中全等三角形共有( )| A、2对 | B、3对 | C、4对 | D、5对 |
 如图,在锐角三角形ABC中,CM为AB边上的高,P为BC的中点,连接MP,在AC上找到一点N,使NP=MP,连接BN,试判断BN与AC的位置关系,并说明理由.
如图,在锐角三角形ABC中,CM为AB边上的高,P为BC的中点,连接MP,在AC上找到一点N,使NP=MP,连接BN,试判断BN与AC的位置关系,并说明理由. 已知两弧长的和l=8π,∠BAC=90°,求半圆形的周长.
已知两弧长的和l=8π,∠BAC=90°,求半圆形的周长. 已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题:
已知一次函数y=kx+b的图象是直线l,根据图象解答下列问题: 如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S. 如图,数轴上表示1、
如图,数轴上表示1、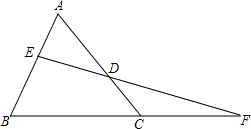 如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.
如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.