题目内容
8.在四边形ABCD中,有下列条件:①AB$\stackrel{∥}{=}$CD;②AD$\stackrel{∥}{=}$BC;③AC=BD;④AC⊥BD.(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是$\frac{1}{2}$.
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断能判定四边形ABCD是矩形和是菱形的概率是否相等?
分析 (1)根据概率即可得到结论;
(2)列表得出所有等可能的情况数,找出能判定四边形ABCD是矩形和菱形的情况数,即可求出所求的概率.
解答  解:(1)①或②能判定四边形ABCD是平行四边形,
解:(1)①或②能判定四边形ABCD是平行四边形,
故$\frac{2}{4}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$;
(2)画树状图如图所示,
由树状图得知,从中任选两个作为已知条件共有12结果,能判定四边形ABCD是矩形的有4种,能判定四边形ABCD是菱形的有4种,
∴能判定四边形ABCD是矩形的概率=$\frac{4}{12}$=$\frac{1}{3}$,能判定四边形ABCD是菱形的概率=$\frac{4}{12}$=$\frac{1}{3}$,
∴判断能判定四边形ABCD是矩形和是菱形的概率相等.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.如果a<b<0,那么下列不等式中成立的是( )
| A. | -3a<-3b | B. | a3<b3 | C. | a2<b2 | D. | c-a<c-b |
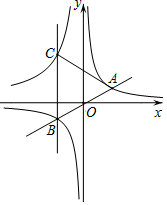 如图,过点O的直线AB与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=$\frac{-3k}{x}$(x<0)的图象交于点C,连接AC,则△ABC的面积为8.
如图,过点O的直线AB与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=$\frac{-3k}{x}$(x<0)的图象交于点C,连接AC,则△ABC的面积为8.