题目内容
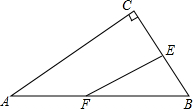如图，在△ABC中，AC⊥BC，AB=10cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜5）．（1）t=
（2）t=
（3）t=
考点：相似三角形的判定,线段垂直平分线的性质,等腰三角形的判定
专题：动点型
分析：（1）用t表示出BF及BE的长，根据相似三角形的对应边成比例即可得出t的值；
（2）分BF=BE，BF=EF与BE=EF三种情况进行讨论；
（3）连接AE，根据EF的垂直平分线过点A可知AE=AF，再根据勾股定理求出AC的长，进而可得出结论．
（2）分BF=BE，BF=EF与BE=EF三种情况进行讨论；
（3）连接AE，根据EF的垂直平分线过点A可知AE=AF，再根据勾股定理求出AC的长，进而可得出结论．
解答：解：（1）∵F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，
∴BF=10-2t，BE=t，
∴当△BEF∽△BCA时，
=
，即
=
，解得t=
（秒）；
当△BEF∽△BAC时，
=
，即
=
，解得t=
（秒）．
综上所示，当t=
秒或t=
秒时，△BEF与△ABC相似．
故答案为：
秒或
秒；
（2）当BF=BE时，
∵BF=10-2t，BE=t，
∴10-2t=t，解得t=
（秒）；
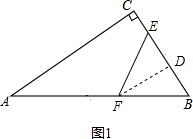
当BF=EF时，如图1所示，
过点F作FD⊥BC于点D，则BD=
BE=
，
∵AC⊥BC，
∴DF∥AC，
∴cosB=
=
，即
=
，解得t=
（秒）；
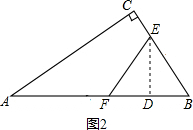当BE=EF时，如图2所示，过点E作ED⊥AB于点D，则BD=
BF=5-t，
∵AC⊥BC，
∴cosB=
=
，即
=
．解得t=
（秒）．
综上所述，t=
秒或
秒或
秒时，△BEF为等腰三角形．
故答案为：
秒或
秒或
秒；
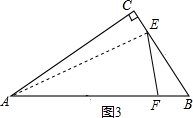（3）如图3所示，连接AE，
∵EF的垂直平分线过点A，
∴AE=AF．
∵AC⊥BC，AB=10cm，BC=6cm，
∴AC=
=8cm．
∵AF=2t，CE=6-t，
∴2t=
，解得t=（
-2）秒．
故答案为：（
-2）秒．
∴BF=10-2t，BE=t，
∴当△BEF∽△BCA时，
| BE |
| BC |
| BF |
| AB |
| t |
| 6 |
| 10-2t |
| 10 |
| 30 |
| 11 |
当△BEF∽△BAC时，
| BE |
| AB |
| BF |
| BC |
| t |
| 10 |
| 10-2t |
| 6 |
| 50 |
| 13 |
综上所示，当t=
| 30 |
| 11 |
| 50 |
| 13 |
故答案为：
| 30 |
| 11 |
| 50 |
| 13 |
（2）当BF=BE时，
∵BF=10-2t，BE=t，
∴10-2t=t，解得t=| 10 |
| 3 |
当BF=EF时，如图1所示，
过点F作FD⊥BC于点D，则BD=
| 1 |
| 2 |
| t |
| 2 |
∵AC⊥BC，
∴DF∥AC，
∴cosB=
| BD |
| BF |
| BC |
| AB |
| ||
| 10-2t |
| 6 |
| 10 |
| 60 |
| 17 |
当BE=EF时，如图2所示，过点E作ED⊥AB于点D，则BD=| 1 |
| 2 |
∵AC⊥BC，
∴cosB=
| BD |
| BE |
| BC |
| AB |
| 5-t |
| t |
| 6 |
| 10 |
| 25 |
| 8 |
综上所述，t=
| 10 |
| 3 |
| 60 |
| 17 |
| 25 |
| 8 |
故答案为：
| 10 |
| 3 |
| 60 |
| 17 |
| 25 |
| 8 |
（3）如图3所示，连接AE，∵EF的垂直平分线过点A，
∴AE=AF．
∵AC⊥BC，AB=10cm，BC=6cm，
∴AC=
| 102-62 |
∵AF=2t，CE=6-t，
∴2t=
| 82+(6-t)2 |
4
| ||
| 3 |
故答案为：（
4
| ||
| 3 |
点评：本题考查的是相似三角形的判定，在解答此题时要进行分类讨论，不要漏解．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
下列各数值是方程-2x=10的解的是（ ）
| A、x=-3 | B、x=-5 |
| C、x=0 | D、x=5 |
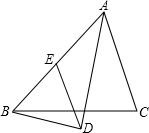在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC交AB于E．