题目内容
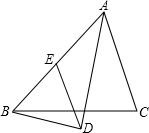 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.(1)求证:DE=BE;
(2)若AB=10,求线段DE的长.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)证明∠EAD=∠EDA,此为解题的关键性结论;证明∠EAD=∠EDA,即可解决问题.
(2)证明DE为直角△ABD斜边的中线,即可解决问题.
(2)证明DE为直角△ABD斜边的中线,即可解决问题.
解答: 解:(1)∵AD平分∠BAC,DE∥AC,
解:(1)∵AD平分∠BAC,DE∥AC,
∴∠EAD=∠CAD,∠EDA=∠CAD,
∴∠EAD=∠EDA,
∵BD⊥AD,
∴∠EBD+∠EAD=∠BDE+∠EDA
∴∠EBD=∠BDE,
∴DE=BE.
(2)∵∠EAD=∠EDA,
∴DE=AE,而DE=BE,
∴DE=
AB=
×10=5.
 解:(1)∵AD平分∠BAC,DE∥AC,
解:(1)∵AD平分∠BAC,DE∥AC,∴∠EAD=∠CAD,∠EDA=∠CAD,
∴∠EAD=∠EDA,
∵BD⊥AD,
∴∠EBD+∠EAD=∠BDE+∠EDA
∴∠EBD=∠BDE,
∴DE=BE.
(2)∵∠EAD=∠EDA,
∴DE=AE,而DE=BE,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题主要考查了等腰三角形的判定与性质、直角三角形的性质、平行线的性质等几何知识点的应用问题;灵活运用有关定理来分析、判断是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、8的立方根是±2 | ||
B、
| ||
| C、1的平方根是1 | ||
D、
|
 已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC.
已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC. 如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.
如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.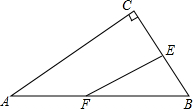 如图,在△ABC中,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在△ABC中,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,