题目内容
1. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )
如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )| A. | 2π | B. | $\frac{8}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{3}{8}$π |
分析 根据垂径定理求得CE=ED=2$\sqrt{3}$,然后由圆周角定理知∠DOE=60°,然后通过解直角三角形求得线段OD、OE的长度,最后将相关线段的长度代入S阴影=S扇形ODB-S△DOE+S△BEC.
解答  解:如图,假设线段CD、AB交于点E,
解:如图,假设线段CD、AB交于点E,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2$\sqrt{3}$,
又∵∠BCD=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=DE•cot60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,OD=2OE=4,
∴S阴影=S扇形ODB-S△DOE+S△BEC=$\frac{60π×{OD}^{2}}{360}$-$\frac{1}{2}$OE×DE+$\frac{1}{2}$BE•CE=$\frac{8π}{3}$-2$\sqrt{3}$+2$\sqrt{3}$=$\frac{8π}{3}$.
故选B.
点评 考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,地球的体积约是太阳体积的倍数是( )
| A. | 7.1×10-6 | B. | 7.1×10-7 | C. | 1.4×106 | D. | 1.4×107 |
9. 某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
 某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )| A. | 19,20,14 | B. | 19,20,20 | C. | 18.4,20,20 | D. | 18.4,25,20 |
16. 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
11.已知点A(2,y1)、B(4,y2)都在反比例函数y=$\frac{k}{x}$(k<0)的图象上,则y1、y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
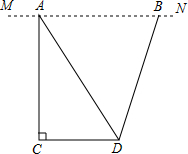 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离($\sqrt{3}$取1.73,结果精确到0.1千米)
如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离($\sqrt{3}$取1.73,结果精确到0.1千米)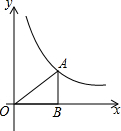 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为2$\sqrt{6}$+4.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为2$\sqrt{6}$+4. 如图,已知△ABC中,∠ABC=90°
如图,已知△ABC中,∠ABC=90°