题目内容
6.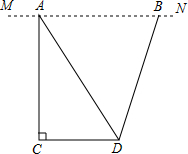 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离($\sqrt{3}$取1.73,结果精确到0.1千米)
如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离($\sqrt{3}$取1.73,结果精确到0.1千米)
分析 过B作BE⊥AD于E,三角形的内角和得到∠ADB=45°,根据直角三角形的性质得到AE=2.BE=2$\sqrt{3}$,求得AD=2+2$\sqrt{3}$,即可得到结论.
解答  解:过B作BE⊥AD于E,
解:过B作BE⊥AD于E,
∵∠NAD=60°,∠ABD=75°,
∴∠ADB=45°,
∵AB=6×$\frac{40}{60}$=4,
∴AE=2.BE=2$\sqrt{3}$,
∴DE=BE=2$\sqrt{3}$,
∴AD=2+2$\sqrt{3}$,
∵∠C=90,∠CAD=30°,
∴CD=$\frac{1}{2}$AD=1+$\sqrt{3}$≈2.7千米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
1. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )
如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )
 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )
如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4$\sqrt{3}$,则S阴影=( )| A. | 2π | B. | $\frac{8}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{3}{8}$π |
11.已知M=$\frac{2}{9}$a-1,N=a2-$\frac{7}{9}$a(a为任意实数),则M、N的大小关系为( )
| A. | M<N | B. | M=N | C. | M>N | D. | 不能确定 |
16.下列运算正确的是( )
| A. | a2•a3=a6 | B. | 5a-2a=3a2 | C. | (a3)4=a12 | D. | (x+y)2=x2+y2 |
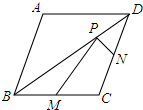 如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$.
如图,已知菱形ABCD的两条对角线长分别是3和4,点M、N分别是边BC、CD的中点,点P是对角线上的一点,则PM+PN的最小值是$\frac{5}{2}$. 如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC. 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,AB=12$\sqrt{3}$,OP=6,则劣弧AB的长为8π.
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,AB=12$\sqrt{3}$,OP=6,则劣弧AB的长为8π.