Question

13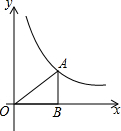．如图，点A在函数y=$\frac{4}{x}$（x＞0）的图象上，且OA=4，过点A作AB⊥x轴于点B，则△ABO的周长为2$\sqrt{6}$+4．

Answer 1

分析 由点A在反比例函数的图象上，设出点A的坐标，结合勾股定理可以表现出OA²=AB²+OB²，再根据反比例函数图象上点的坐标特征可得出AB•OB的值，根据配方法求出（AB+OB）²，由此即可得出AB+OB的值，结合三角形的周长公式即可得出结论．

解答 解：∵点A在函数y=$\frac{4}{x}$（x＞0）的图象上，
∴设点A的坐标为（n，$\frac{4}{n}$）（n＞0）．
在Rt△ABO中，∠ABO=90°，OA=4，
∴OA²=AB²+OB²，
又∵AB•OB=$\frac{4}{n}$•n=4，
∴（AB+OB）²=AB²+OB²+2AB•OB=4²+2×4=24，
∴AB+OB=2$\sqrt{6}$，或AB+OB=-2$\sqrt{6}$（舍去）．
∴C_△ABO=AB+OB+OA=2$\sqrt{6}$+4．
故答案为：2$\sqrt{6}$+4．

点评 本题考查了反比例函数图象上点的坐标特征、完全平方公式以及三角形的周长，解题的关键是求出AB+OB的值．本题属于基础题，难度不大，解决该题型题目时，巧妙的利用完全平方公式直接求出两直角边之和是关键．