题目内容
11．在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子，围棋子除颜色外其余均相同．从这个盒子中随机地摸出1个围棋子，记下颜色后放回，搅匀后再随机地摸出1个围棋子记下颜色．请用画树状图（或列表）的方法，求两次摸出的围棋子颜色都是白色的概率．分析 首先根据题意列出表格，然后由表格即可求得所有等可能的结果与两次摸出的围棋子颜色都是白色的情况，再利用概率公式即可求得答案．
解答 解：列表得：
| 第一次 第二次 | 白1 | 白2 | 黑 |
| 白1 | （白1，白1） | （白2，白1） | （黑，白1） |
| 白2 | （白1，白2） | （白2，白2） | （黑，白2） |
| 黑 | （白1，黑） | （白2，黑） | （黑，黑） |
∴P（两次摸出的围棋子颜色都是白色）=$\frac{4}{9}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．计算（-3）3的结果等于（ ）
| A． | 9 | B． | -9 | C． | 27 | D． | -27 |
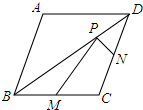如图，已知菱形ABCD的两条对角线长分别是3和4，点M、N分别是边BC、CD的中点，点P是对角线上的一点，则PM+PN的最小值是$\frac{5}{2}$．
如图，在矩形ABCD中，AD=9cm，AB=3cm，将其折叠，使点D与点B重合，则重叠部分（△BEF）的面积为7.5cm2．
1．
如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=4$\sqrt{3}$，则S阴影=（ ）
如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=4$\sqrt{3}$，则S阴影=（ ）| A． | 2π | B． | $\frac{8}{3}$π | C． | $\frac{4}{3}$π | D． | $\frac{3}{8}$π |