题目内容
 如图,在△ABC中,∠ABC=90°,AB=BC,D是AC上一点,CF⊥BD于点F,AE⊥BD交BD的延长线于E.求证:EF=BE-AE.
如图,在△ABC中,∠ABC=90°,AB=BC,D是AC上一点,CF⊥BD于点F,AE⊥BD交BD的延长线于E.求证:EF=BE-AE.考点:全等三角形的判定与性质
专题:证明题
分析:利用已知条件易证△ABE≌△BCF,所以CF=BE,AE=BF,进而可证明EF=BE-AE.
解答:证明:∵CF⊥BD于点F,AE⊥BD,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
又∵∠ABC=90°,
∴∠ABE+∠CBE=90°,
∴∠BAE=∠CBF,
在三角形ABE和BCF中,
,
∴△ABE≌△BCF(AAS),
∴CF=BE,AE=BF,
∴EF=BE-AE.
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
又∵∠ABC=90°,
∴∠ABE+∠CBE=90°,
∴∠BAE=∠CBF,
在三角形ABE和BCF中,
|
∴△ABE≌△BCF(AAS),
∴CF=BE,AE=BF,
∴EF=BE-AE.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.

练习册系列答案
相关题目
化简(
-2)2008×(2+
)2009的结果是( )
| 3 |
| 3 |
| A、-l | ||
B、
| ||
C、
| ||
D、-
|
能使
=
成立的取值范围是( )
|
| ||
|
| A、a>3 | B、a≥0 |
| C、0≤a<3 | D、a<3或a>3 |

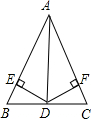 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,BE=CF,求证:D是BC的中点.
如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,BE=CF,求证:D是BC的中点.