题目内容

13．解方程：x2+3x=5x+15．

分析 先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式（x-5）（x+3）=0，进而可得x-5=0，x+3=0，再解即可；

解答 解：x2+3x=5x+15，
x2-2x-15=0，
（x-5）（x+3）=0，
x-5=0，x+3=0，
解得：x1=5，x2=-3．

点评 此题主要考查了因式分解法解一元二次方程，关键是掌握因式分解法解一元二次方程的一般步骤：①移项，使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零，得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解．

练习册系列答案
相关题目
12．已知，在三角形ABC中，点D在BC上，DE⊥AB于E，点F在AB上，在CF的延长线上取一点G，连接AG．
（1）如图1，若∠GAB=∠B，∠GAC+∠EDB=180°，求证：AB⊥AC．
（2）如图2．在（1）的条件下，∠GAC的平分线交CG于点M，∠ACB的平分线交AB于点N，当∠AMC-∠ANC=35°时，求∠AGC的度数．
13．解方程：
（1）3（x-1）-7（x+5）=30（x+1）
（2）$\left\{\begin{array}{l}{2x+y=1}\\{3x-2y=-9}\end{array}\right.$．
1．为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接收方由密文→明文（解密）．已知加密规则为：明文a，b，c对应密文a+2b，2b+c，3c．例如：明文1，2，3对应的密文5，7，9．当接收方收到密文14，9，15时，则解密得到的明文为（　　）
A．10，5，2B．10，2，5C．2，5，10D．5，10，2
8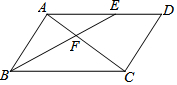．如图，在?ABCD中，BC=5，AB=3，BE平分∠ABC交AD于点E，交对角线AC于点F，则$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=$\frac{9}{25}$．
18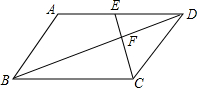．如图，在平行四边形ABCD中，E为AD的中点，△DEF的周长为1，则△BCF的周长为（　　）
A．1B．2C．3D．4
5．解方程：
（1）x2+2x-1=0
（2）3x2-18x-10=0
（3）-3x2+22x-24=0．
2．把下列各数填在相应的大括号中
5%，0，25，-9，2π，$\frac{22}{7}$，1.213，$-\frac{3}{4}$，3.121121112…．
（1）正数集合：{5%，25，2π，$\frac{22}{7}$，1.213，3.121121112… …}；
（2）正分数集合：{5%，$\frac{22}{7}$，1.213…}；
（3）非负整数集合：{0，25…}；
（4）无理数集合：{2π，3.121121112……}．
3．实数-$\sqrt{4}$，0，$\frac{22}{7}$，$\root{3}{-125}$，0.1010010001…（两个1之间依次多一个0），$\frac{49}{121}$，$\frac{π}{2}$中，无理数有0.1010010001…（两个1之间依次多一个0），$\frac{π}{2}$，整数有-$\sqrt{4}$，0，$\root{3}{-125}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网