题目内容
已知△ABC与△DEF,现给出四个条件:①∠A=∠D;②AC=DF;③AB=DE;④△ABC的周长与△DEF的周长相等.
(1)请你以其中的三个条件作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个真命题写在横线上: .
(2)请以其中的两个条件(其中一个必须是条件④,另一个自选)作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个假命题写在横线上: .并举一个反例说明.
(1)请你以其中的三个条件作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个真命题写在横线上:
(2)请以其中的两个条件(其中一个必须是条件④,另一个自选)作为命题的已知条件,以“△ABC≌△DEF”作为命题的结论,将一个假命题写在横线上:
考点:命题与定理,全等三角形的判定
专题:
分析:(1)如果已知①②③,利用SAS易证△ABC≌△DEF,从而可得真命题;
(2)如果已知②④,那么不能得出△ABC≌△DEF,举反例即可证明.
(2)如果已知②④,那么不能得出△ABC≌△DEF,举反例即可证明.
解答:解:(1)真命题为:如果∠A=∠D,AC=DF,AB=DE,那么△ABC≌△DEF.
证明:在△ABC和△DEF中,
,
∴△ABC≌△DEF;
(2)假命题为:如果AC=DF,△ABC的周长与△DEF的周长相等,那么△ABC≌△DEF.
例如,在△ABC和△DEF中,AC=DF=4,AB=3,BC=5,DE=EF=4,此时△ABC是不等边三角形,而△DEF是等边三角形,所以△ABC与△DEF不全等.
故答案为:如果∠A=∠D,AC=DF,AB=DE,那么△ABC≌△DEF;如果AC=DF,△ABC的周长与△DEF的周长相等,那么△ABC≌△DEF.
证明:在△ABC和△DEF中,
|
∴△ABC≌△DEF;
(2)假命题为:如果AC=DF,△ABC的周长与△DEF的周长相等,那么△ABC≌△DEF.
例如,在△ABC和△DEF中,AC=DF=4,AB=3,BC=5,DE=EF=4,此时△ABC是不等边三角形,而△DEF是等边三角形,所以△ABC与△DEF不全等.
故答案为:如果∠A=∠D,AC=DF,AB=DE,那么△ABC≌△DEF;如果AC=DF,△ABC的周长与△DEF的周长相等,那么△ABC≌△DEF.
点评:此题考查了命题与定理,全等三角形的判定.解题的关键是掌握判定两三角形全等的方法:AAS,ASA,SAS,SSS,是直角三角形的还有HL.

练习册系列答案
相关题目
若关于x的方程
=1-
有增根,则k的值为( )
| 3 |
| x-1 |
| k |
| 1-x |
| A、3 | B、1 | C、0 | D、-1 |
 如图,一次函数y=-2x+12分别与x轴、y轴交于点A、B,点C是线段AB的中点,点D在线段OC上,且OD=2CD.
如图,一次函数y=-2x+12分别与x轴、y轴交于点A、B,点C是线段AB的中点,点D在线段OC上,且OD=2CD.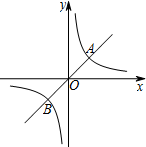 如图,定义:若双曲线y=
如图,定义:若双曲线y= 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.