题目内容
5.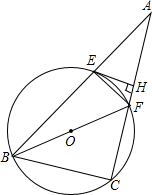 已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.
已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.(1)求证:△AEF∽△ACB.
(2)若AE=$2\sqrt{5}$,AF=5,BC=4,AC=8,连结BF.
①求证:BF为直径;
②过E作EH⊥AC,垂足为H.求证:EH与⊙O相切.
分析 (1)由圆内接四边形的性质可知∠ABC=∠AFE,从而根据∠A=∠A,∠ABC=∠AFE可证明△AEF∽△ACB;
(2)①由相似三角形的性质先求得AB=4$\sqrt{5}$,在△ACB中,利用勾股定理的逆定理可证明△ABC为直角三角形,故此BF为圆O的直径;②连接OE.由△AEF∽△ACB,∠C=90°,可求得∠AEF=90°,在Rt△AEF中,利用勾股定理求得EF=$\sqrt{5}$,然后由BE=AB-AE得到BE=2$\sqrt{5}$,从而可知EF是AB的垂直平分线,从而得到BF=AF,于是有∠A=∠ABF,接下来证明∠FEH=∠A=∠ABF,故此∠HEF+∠OEF=∠ABF+∠EFB=90°,从而得到EH是圆O的切线.
解答 证明:(1)∵四边形BCFE是圆O的内接四边形,
∴∠ABC=∠AFE.
又∵∠A=∠A
∴△AEF∽△ACB.
(2)①∵△AEF∽△ACB,
∴$\frac{AB}{AC}=\frac{AF}{AE}$.
∴$\frac{AB}{8}=\frac{5}{2\sqrt{5}}$.
解得:AB=4$\sqrt{5}$.
∵AB=4$\sqrt{5}$,AC=8,BC=4.
∴AB2=AC2+BC2.
∴△ABC为直角三角形.
∴∠C=90°.
∴BF是圆O的直径.
②连接OE.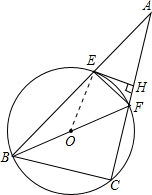
∵BF是圆O的直径,
∴∠FEB=90°.
∴EF⊥AB.
∵BE=AB-AE=4$\sqrt{5}$-2$\sqrt{5}$=2$\sqrt{5}$,
∴BE=AE.
∴EF是AB的垂直平分线.
∴BF=AF.
∴∠A=∠ABF.
∵OE=OF,
∴∠OEF=∠OFE.
∴∠A+∠OEF=∠EBF+∠BFE=90°.
∵EH⊥AC,
∴∠HEF+∠EFH=90°.
又∵∠FEA+∠A=90°
∴∠HEF=∠A.
∴∠HEF+∠OEF=90°,即∠OEH=90°.
∴EH与⊙O相切.
点评 本题主要考查的圆的性质、圆周角定理、切线的判定、勾股定理和勾股定理的逆定理的应用、相似三角形的性质和判定、线段垂直平分线的性质的应用,证得∠OEH=90°是解题的关键.

| A. | 5,2,3 | B. | 10,5,4 | C. | 4,8,4 | D. | 2,3,4 |
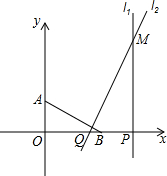 如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒
如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒