题目内容
16.已知二次函数y=-x2+ax-4的图象的最高点在x轴上,则该点的坐标是(2,0)或(-2,0).分析 根据题意得到该抛物线的顶点坐标在x轴上,则由此求得a的值,结合函数解析式可以得到该点的坐标.
解答 解:∵二次函数y=-x2+ax-4的图象最高点在x轴上,
∴二次函数图象与x轴只有一个交点,
令y=0可得-x2+ax-4=0,则该一元二次方程有两个相等的实数根,
∴△=0,即a2-16=0,
解得a=±4,
∴二次函数关系式为y=-x2+4x-4=-(x-2)2或y=-x2-4x-4=-(x+2)2,
∴该点的坐标是(2,0)或(-2,0).
故答案是:(2,0)或(-2,0).
点评 本题主要考查二次函数的最值,掌握二次函数的顶点在x轴上则二次函数与x轴的交点只有一个是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
6.如果m-n=3,mn=1,那么m2+n2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
 作图题:
作图题: 画出如图所示的几何体的三视图.
画出如图所示的几何体的三视图.
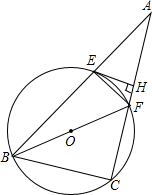 已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.
已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.