题目内容
5.计算:(1)3$\sqrt{3}$-$\sqrt{8}+\sqrt{2}-\sqrt{27}$;
(2)(2$\sqrt{5}+5\sqrt{2})(2\sqrt{5}-5\sqrt{2})-(\sqrt{5}-\sqrt{2})^{2}$(2$\sqrt{5}-5\sqrt{2})-(\sqrt{5}-\sqrt{2})^{2}$-($\sqrt{5}-\sqrt{2})^{2}$2;
(3)$\sqrt{\frac{3}{2}}-(\frac{5}{2}\sqrt{\frac{3}{2}}+3\sqrt{\frac{1}{6}}-\sqrt{6})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式和完全平方公式计算;
(3)先把各二次根式化为最简二次根式,然后去括号后合并即可.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$
=-$\sqrt{2}$;
(2)原式=20-50-(5-2$\sqrt{10}$+2)
=-30-7+2$\sqrt{10}$
=-37+2$\sqrt{10}$;
(3)原式=$\frac{\sqrt{6}}{2}$-$\frac{5\sqrt{6}}{4}$-$\frac{\sqrt{6}}{2}$+$\sqrt{6}$
=-$\frac{\sqrt{6}}{4}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
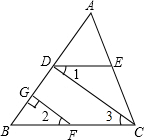 如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明:∠CDE=∠BFG.
如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明:∠CDE=∠BFG. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.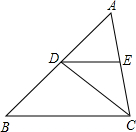 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数. 如图,AB∥CD,∠1=∠2,试说明∠E与∠F的关系.
如图,AB∥CD,∠1=∠2,试说明∠E与∠F的关系.