题目内容
6.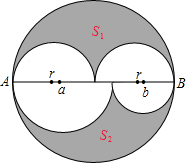 如图,大圆的半径为r,直径AB上方两个半圆的直径均为r,下方两个半圆的直径分别为a,b.
如图,大圆的半径为r,直径AB上方两个半圆的直径均为r,下方两个半圆的直径分别为a,b.(1)求直径AB上方阴影部分的面积S1;
(2)用含a,b的代数式表示直径AB下方阴影部分的面积S2=$\frac{1}{4}πab$;
(3)设a=r+c,b=r-c(c>0),那么( )
(A)S2=S1;(B)S2>S1;(C)S2<S1;(D)S2与S1的大小关系不确定;
(4)请对你在第(3)小题中所作的判断说明理由.
分析 (1)用半径为r的半圆的面积减去直径为r的圆的面积即可;
(2)用直径为(a+b)的半圆的面积减去直径为a的半圆的面积,再减去直径为b的半圆的面积即可;
(3)(4)将a=r+c,b=r-c,代入S2,然后与S1比较即可.
解答 解:(1)S1=$\frac{1}{2}π{r}^{2}$-$\frac{1}{4}π{r}^{2}$=$\frac{1}{4}π{r}^{2}$;
(2)S2=$\frac{1}{2}$π($\frac{a+b}{2}$)2-$\frac{1}{2}$$•\frac{1}{4}$πa2-$\frac{1}{2}•$$\frac{1}{4}$πb2,
=$\frac{1}{8}$π(a+b)2-$\frac{1}{8}$πa2-$\frac{1}{8}π{b}^{2}$
=$\frac{1}{4}πab$,
故答案为:$\frac{1}{4}πab$;
(3)选:C;
(4)将a=r+c,b=r-c,代入S2,得:
S2=$\frac{1}{4}π$(r+c)(r-c)=$\frac{1}{4}π$(r2-c2),
∵c>0,
∴r2>r2-c2,
即S1>S2.
故选C.
点评 此题考查了列代数式表示图形的面积,解题的关键是:结合图形分清各个半圆的半径及熟记圆的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某公司准备投资开发A、B两种新产品,信息部通过市场调研得到两条信息:
信息一:如果投资A种产品,所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:y=kx;
信息二:如果投资B种产品,所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
根据公司信息部报告,yA、yB(万元)与投资金额x(万元)的部分对应值如上表所示:
(1)填空:yA=0.6x; yB=-0.2x2+2.6x;
(2)如果公司准备投资15万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),试求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
| x(万元) | 1 | 2 |
| yA(万元) | 0.6 | 1.2 |
| yB(万元) | 2.4 | 4.4 |
信息二:如果投资B种产品,所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
根据公司信息部报告,yA、yB(万元)与投资金额x(万元)的部分对应值如上表所示:
(1)填空:yA=0.6x; yB=-0.2x2+2.6x;
(2)如果公司准备投资15万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),试求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.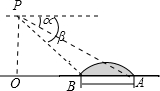 如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)
如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m) 如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,求△DBC的面积.
如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,求△DBC的面积. 如图,AB∥CD,∠1=∠2,试说明∠E与∠F的关系.
如图,AB∥CD,∠1=∠2,试说明∠E与∠F的关系.