题目内容
18.AB为⊙O的直径,点P在⊙O外,PC、PD分别切⊙O于点C、D,连接OC、OD.(1)如图1,求证:∠P+∠COD=180°;
(2)如图2,连接AD、BC、AD交BC于点E,求证:∠AEC=$\frac{1}{2}$∠P;
(3)如图3,在(2)的条件下,延长PC、交BA的延长线于点H,设OC与AD的交点为F,OD与BC的交点为G,若PC+PD=AB,CH=2CF,OF=4,求线段OG的长.

分析 (1)直接利用切线的性质得出OC⊥PC,OD⊥PD,进而利用四边形内角和定理得出答案;
(2)利用圆周角定理结合三角形的外角的性质得出答案;
(3)首选利用正方形的判定与性质得出∠PCO=∠COD=90°,进而得出△COK≌△ODF(AAS),再利用勾股定理以及平行线的性质得出OG的长.
解答 (1)证明:∵PC、PD分别切⊙O于点C、D,
∴OC⊥PC,OD⊥PD,
∴∠PCO=∠PDO90°,
∴∠P+∠COD=360°-90°-90°=180°;
(2)证明:∵∠B=$\frac{1}{2}$∠AOC,∠A=$\frac{1}{2}$∠BOD,
∴∠AEC=∠A+∠B=$\frac{1}{2}∠AOC+\frac{1}{2}∠BOD$,
=$\frac{1}{2}$(∠AOC+∠BOD),
=$\frac{1}{2}$(180°-∠COD),
=$\frac{1}{2}$∠P;
(3)解:∵PC、PD分别切⊙O于点C、D,
∴PC=PD,
∵PC+PD=2AB,
∴CO=DO=AO=CO=DO,
∴四边形PCOD是菱形,
∴∠P=∠COD,OD∥PH,
∴∠P=∠COD=90°,
∴四边形PCOD是正方形,
∴∠PCO=∠COD=90°,
如图3,过O作OK⊥AD交PC于点,
∴∠HKO+∠COK=90°,∠DFO+∠COK=90°,
∴∠HKO=∠DFO,
在△COK和△ODF中
$\left\{\begin{array}{l}{∠OKC=∠DFO}\\{∠KCO=∠OD}\\{CO=DO}\end{array}\right.$,
∴△COK≌△ODF(AAS),
∴CK=OF=4,
∵∠DFO+∠ODF=90°,
∴∠COK=∠ODF+∠OAD,
∵∠DFO=∠OAD+∠AOC=∠COK+∠AOC=∠AOK,
∴AK=AO,
设CF=x,则CH=2x,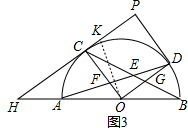
∴HO=HK=2x+4,
在Rt△OCH中,(x+4)2+(2x)2=(2x+4)2,
解得:x=0或x=8,
∴CH=16,BO=OC=4+8=12,HO=HK=20,
∵DO∥HP,
∴$\frac{BO}{HB}$=$\frac{OG}{CH}$,
即:$\frac{12}{32}$=$\frac{GO}{16}$,
∴OG=6.
点评 此题主要考查了圆的综合以及全等三角形的判定与性质和正方形的判定与性质等知识,正确得出FC的长是解题关键.

| A. | (2,-1) | B. | (2,1) | C. | (1,2) | D. | (-1,-2) |

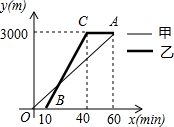 甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:
甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:
