题目内容
1.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.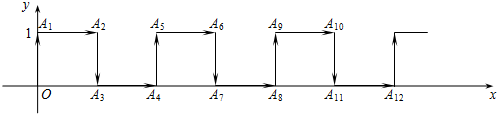
(1)填写下列各点的坐标:A3(1,0)、A7(3,0)、A11(5,0);
(2)写出点A2n+1的坐标(n是奇数);
(3)指出蚂蚁从原点O爬到点(101,1)时,爬行方向经历了多少次向上爬行?
分析 (1)观察图形可知,A3,A7,A11在x轴上,求出OA3、OA7,OA11长度,然后写出坐标即可;
(2)根据(1)中规律写出点A2n+1的坐标即可;
(3)根据每4个点为一个循环组依次循环,可知点A202(101,1),每4个点里面有一次向上爬行,202÷4=50…2,即可解答.
解答 解:(1)由图可知,A3,A7,A11都在x轴上,
∵小蚂蚁每次移动1个单位,
∴OA3=1,OA7=3,OA11=5,
∴A3(1,0),A7(3,0),A11(5,0);
故答案为:2,0;3,0;5,0;
(2)根据(1)的规律可得:A2n+1(n,0);
(3)∵每4个点为一个循环组依次循环,
∴点A202(101,1),
∵每4个点里面有一次向上爬行,且第一次爬行向上,202÷4=50…2,
∴蚂蚁从原点O爬到点(101,1)时,爬行方向经历了50+1=51次向上爬行.
点评 本题考查的是点的坐标,解决本题的关键是观察坐标找到规律.

练习册系列答案
相关题目
10.已知x2-3x+1=0,则$\frac{x}{{{x^2}-x+1}}$的值是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
11.下列各组数据中,不能作为一个直角三角形三边长的一组是( )
| A. | 32,42,52 | B. | $1,\sqrt{2},\sqrt{3}$ | C. | $1,2,\sqrt{3}$ | D. | $1,\sqrt{2},1$ |
 如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
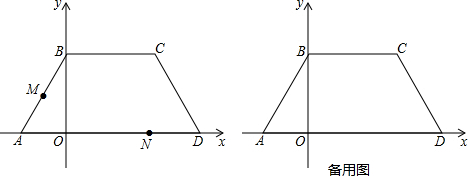
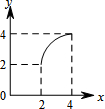
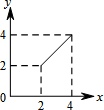
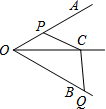 如图,∠AOB=60°,点C在∠AOB的平分线上,OC=4,点P、Q分别是射线OA、OB上不同于O的一点,且四边形OPCQ的内角∠PCQ=120°.设CP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,∠AOB=60°,点C在∠AOB的平分线上,OC=4,点P、Q分别是射线OA、OB上不同于O的一点,且四边形OPCQ的内角∠PCQ=120°.设CP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )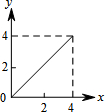

 如图,点A、C的坐标分别为(3,0)、(0,2),分别过点A,C作x轴、y轴的垂线交于点B.
如图,点A、C的坐标分别为(3,0)、(0,2),分别过点A,C作x轴、y轴的垂线交于点B.