题目内容
5.已知a=2013,b=2015,c是一个有理数,求代数式$\frac{1}{2}$(a+c)2+$\frac{1}{2}$(b+c)2-(a+c)(b+c)的值.分析 将原式利用完全平方公式变形,进而代入已知求出答案.
解答 解:∵a=2013,b=2015,
∴$\frac{1}{2}$(a+c)2+$\frac{1}{2}$(b+c)2-(a+c)(b+c)
=$\frac{1}{2}$[(a+c)2+(b+c)2-2(a+c)(b+c)]
=$\frac{1}{2}$(a+c-b-c)2
=$\frac{1}{2}$(2013-2015)2
=2.
点评 此题主要考查了整式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
15.以下条件不能判别四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC,∠A=90° | B. | OA=OB=OC=OD | ||
| C. | AB=CD,AB∥CD,AC=BD | D. | AB=CD,AB∥CD,OA=OC,OB=OD |
13. 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )| A. |  | B. |  | C. | 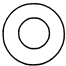 | D. | 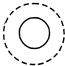 |
15.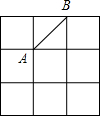 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
 在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )
在边长为2的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为2的概率为( )| A. | $\frac{3}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{16}$ |
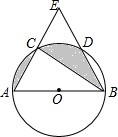 如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.
如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.