��Ŀ����
19��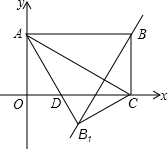 ��ͼ������OABC��ƽ��ֱ������ϵ�У�����OA��OC�ij����㣺|OA-2$\sqrt{3}$|+��OC-6��2=0��
��ͼ������OABC��ƽ��ֱ������ϵ�У�����OA��OC�ij����㣺|OA-2$\sqrt{3}$|+��OC-6��2=0����1����A��B��C��������꣮
��2���ѡ�ABC��AC���ۣ���B���ڵ�B1����AB1��x�ύ�ڵ�D����ֱ��BB1�Ľ���ʽ��
��3����ֱ��AC���Ƿ���ڵ�PʹPB1+PD��ֵ��С�������ڣ����ҳ���P��λ�ã������PB1+PD����Сֵ���������ڣ���˵�����ɣ�
��4����ֱ��AC���Ƿ���ڵ�Pʹ|PD-PB|��ֵ��������ڣ����ҳ���P��λ�ã������|PD-PB|���ֵ��
���� ��1���ɷǸ��������ʿ����OA��OC�ij�����ɵõ�A��C�����꣬���ɾ��ε����ʿ����B�����ꣻ
��2������ԳƵ����ʿ�֪AC��BB1���ɣ�1����֪A��C������꣬�����ֱ��AC�Ľ���ʽ��������ֱ��BB1�Ľ���ʽ��
��3����B��B1����ֱ��AC�Գƿ�֪������BD��ֱ��AC���ڵ�P�����ʱPD+PB=PD+PB1�����������������۵������ʿ�֤����AOD�ա�CB1D����Rt��AOD�п����OD��������CD������Rt��BCD���ɹ��ɶ��������BD�ij���
��4�������������߹�ϵ��֪|PD-PB|��BD��ֻ�е�P�����߶�BD���ӳ����ӳ�����ʱ������|PD-PB|=BD����Ȼ�����������ĵ㣮
��� �⣺��1����|OA-2$\sqrt{3}$|+��OC-6��2=0��
��OA=2$\sqrt{3}$��OC=6��
��A��0��2$\sqrt{3}$����C��6��0����
���ı���OABCΪ���Σ�
��BC=OA=2$\sqrt{3}$��
��B��6��2$\sqrt{3}$����
��2����ֱ��AC�Ľ���ʽΪy=kx+b��
��A��C�������ɵ�$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{6k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
���۵������ʿ�֪AC��BB1��
�����ֱ��BB1�Ľ���ʽΪy=$\sqrt{3}$x+m��
��B���������ɵ�2$\sqrt{3}$=6$\sqrt{3}$+m��
���m=-4$\sqrt{3}$��
��ֱ��BB1�Ľ���ʽΪy=$\sqrt{3}$x-4$\sqrt{3}$��
��3���ɣ�2����֪B��B1����ֱ��AC�Գƣ�
��ͼ1������BD��AC�ڵ�P��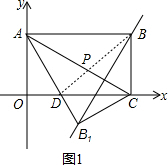
��PB=PB1��
��PD+PB=PD+PB1=BD��
���ʱPD+PB1��С��
���۵������ʿ�֪B1C=BC=OA=2$\sqrt{3}$����AOD=��CB1D=90�㣬
�ڡ�AOD�͡�CB1D�У�
$\left\{\begin{array}{l}{��AOD=��C{B}_{1}C}\\{��ADC=��CD{B}_{1}}\\{AO={B}_{1}C}\end{array}\right.$��
���AOD�ա�CB1D��AAS����
��AD=DC��OD=DB1��
��OD=x����DC=AD=6-x����OA=2$\sqrt{3}$��
��Rt��AOD�У��ɹ��ɶ����ɵ�AO2+OD2=AD2������2$\sqrt{3}$��2+x2=��6-x��2�����x=2��
��CD=AD=6-2=4��
��Rt��BCD�У��ɹ��ɶ����ɵ�BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+��2\sqrt{3}��^{2}}$=2$\sqrt{7}$��
���Ͽ�֪����ʹPB1+PD��ֵ��С�ĵ�P��PB1+PD����СֵΪ2$\sqrt{7}$��
��4����ͼ2������PB��PD��BD��
��p�ڵ�Aʱ|PD-PB|���B��B1�Գƣ�|PD-PB|=|PD-PB1|���������������߹�ϵ|PD-PB1|С�ڻ����DB1����|PD-PB1|�����ֵ����DB1��
��AB1=AB=6��
AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=4��
��DB1=2��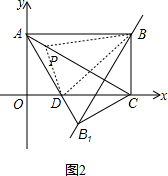
����ֱ��AC�ϣ����ڵ�Pʹ|PD-PB|��ֵ������ֵΪ��2��
���� ������Ҫ����һ�κ������ۺ�Ӧ�ã��漰����ϵ���������ε����ʡ���ԳƵ����ʡ�ȫ�������ε��ж������ʵ�֪ʶ���ڣ�1����ע��Ǹ��������ʵ�Ӧ�ã��ڣ�2�����������ֱ����ֱ�ߵĽ���ʽ�Ĺ�ϵ�ǽ���Ĺؼ����ڣ�3����ȷ����P���λ���ǽ���Ĺؼ����ڣ�4����ע�����������߹�ϵ��Ӧ�ã����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�

| A�� | x6��x2=x3 | B�� | ��x-1y��3=x-3y3 | C�� | 2x3+3x2=6x5 | D�� | ��x+1��2=x2+1 |
| A�� | $\sqrt{-7}$ | B�� | $\root{3}{2}$ | C�� | $\sqrt{{x}^{2}+1}$ | D�� | $\root{3}{\frac{b}{a}}$ |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
| A�� | ��ֱ���������ֱ���ཻ��ͬλ����� | |
| B�� | ��ֱ���������ֱ���ཻ���ڴ������ | |
| C�� | ���������������� | |
| D�� | ��ֱ��ƽ�У�ͬ���ڽ���� |
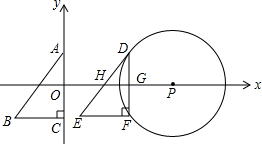
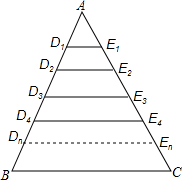 ��ͼ����ABC�У�BC=a��
��ͼ����ABC�У�BC=a��