题目内容
3.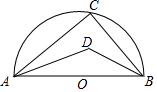 如图,AB=4,以AB为直径作半圆,C为半圆周上一点,D为△ABC内心,△ABD的外接圆半径为2$\sqrt{2}$.
如图,AB=4,以AB为直径作半圆,C为半圆周上一点,D为△ABC内心,△ABD的外接圆半径为2$\sqrt{2}$.
分析 根据圆周角定理得到∠ACB=90°,根据内心的性质得到∠ADB=135°,根据圆内接四边形的性质、圆周角定理得到∠AIB=90°,根据等腰直角三角形的性质计算即可.
解答 解:∵AB为半圆的直径,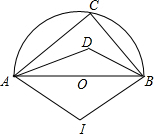
∴∠ACB=90°,
∵D为△ABC内心,
∴∠DAB=$\frac{1}{2}$∠CAB,∠DBA=$\frac{1}{2}$∠CBA,
∴∠ADB=180°-(∠DAB+∠DBA)=180°-45°=135°,
设△ABD的外接圆的圆心为I,
则∠AIB=90°,
∴△ABD的外接圆的半径为:4×sin45°=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查的是三角形的外接圆和外心、内切圆与内心,掌握圆周角定理、圆内接四边形的性质、勾股定理是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.在下列函数中,y是x的反比例函数的是( )
| A. | y=x-1 | B. | y=$\frac{8}{x^2}$ | C. | y=-2x-1 | D. | $\frac{y}{x}$=2 |
14.下列说法正确的是( )
| A. | 将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛物线的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有两个不相等的实数根 | |
| C. | 平行四边形既是中心对称图形又是轴对称图形 | |
| D. | 平分弦的直径垂直于弦,并且平分这条弦所对的两条弧 |
18. 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )| A. | x<3 | B. | x>2 | C. | x<5 | D. | x>5 |
 如图,直线a∥b,∠1=85°,∠2=35°,则∠3为50°.
如图,直线a∥b,∠1=85°,∠2=35°,则∠3为50°.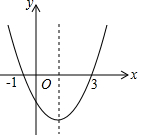 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有5个
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列6个结论正确的有5个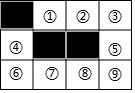 在由相同的小正方形组成的3×4的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形中,其中两个可以由另外两个平移得到,则还需要涂黑的小正方形序号是( )
在由相同的小正方形组成的3×4的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形中,其中两个可以由另外两个平移得到,则还需要涂黑的小正方形序号是( )