题目内容
 科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:| 温度t/℃ | -4 | -2 | 0 | 1 | 4 |
| 植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
考点:二次函数的应用
专题:图表型
分析:首先利用待定系数法求二次函数解析式解析式,在利用二次函数最值公式求法得出即可.
解答:解:设 l=at2+bt+c (a≠0),选(0,49),(1,46),(4,25)代入后得方程组
,
解得:
,
所以l与t之间的二次函数解析式为:l=-t2-2t+49,
当t=-
=-1时,l有最大值50,
即说明最适合这种植物生长的温度是-1℃.
另法:由(-2,49),(0,49)可知抛物线的对称轴为直线t=-1,故当t=-1时,植物生长的温度最快.
故答案为:-1.
|
解得:
|
所以l与t之间的二次函数解析式为:l=-t2-2t+49,
当t=-
| b |
| 2a |
即说明最适合这种植物生长的温度是-1℃.
另法:由(-2,49),(0,49)可知抛物线的对称轴为直线t=-1,故当t=-1时,植物生长的温度最快.
故答案为:-1.
点评:此题主要考查了二次函数的应用以及待定系数法求二次函数解析式,得出二次函数解析式是解题关键.

练习册系列答案
相关题目
 如图,在?ABCD中,∠BAD的平分线AE交BC的延长线于点E,AB=10,BC=6,则CE的长为( )
如图,在?ABCD中,∠BAD的平分线AE交BC的延长线于点E,AB=10,BC=6,则CE的长为( )| A、1 | B、2 | C、3 | D、4 |

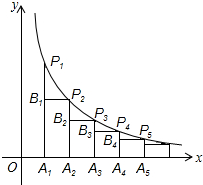 如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y= 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为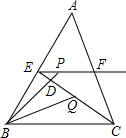 如图,在△ABC中,BC=6
如图,在△ABC中,BC=6