题目内容
1.在△ABC中,AB=AC=10,cosB=$\frac{3}{5}$,如果圆O的半径为2$\sqrt{10}$,且经过点B、C,那么线段AO的长等于6或10.分析 作AD⊥BC于D,如图,利用等腰三角形的性质可判断AD垂直平分BC,则根据垂径定理得到点O在AD上,连接OB,如图,根据余弦的定义可计算出BD=6,则利用勾股定理可计算出AD=8,OD=2,讨论:OA=AD-OD=6;OA=AD+OD=10.
解答 解: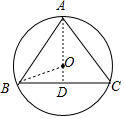 作AD⊥BC于D,如图,
作AD⊥BC于D,如图,
∵AB=AC,
∴AD垂直平分BC,
∴点O在AD上,连接OB,如图,
在Rt△ABD中,cosB=$\frac{BD}{AB}$=$\frac{3}{5}$,
∴BD=10×$\frac{3}{5}$=6,
∴AD=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
在Rt△BOD中,OD=$\sqrt{(2\sqrt{10})^{2}-{6}^{2}}$=2,
∴OA=AD-OD=8-2=6.
或OA=AD+OD=8+2=10.
故答案为6或10.
点评 本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
6.我们规定以下三种变换:
(1)f(a,b)=(-a,b).如:f(1,3)=(-1,3);
(2)g(a,b)=(b,a).如:g(1,3)=(3,1);
(3)h(a,b)=(-a,-b).如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),
求f(h(5,-3))=( )
(1)f(a,b)=(-a,b).如:f(1,3)=(-1,3);
(2)g(a,b)=(b,a).如:g(1,3)=(3,1);
(3)h(a,b)=(-a,-b).如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),
求f(h(5,-3))=( )
| A. | (5,-3) | B. | (-5,3) | C. | (5,3) | D. | (3,5) |
11.如果三角形的一个外角的平分线平行于三角形的一边,那么这个三角形是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
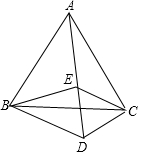 如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.
如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.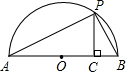 已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.