题目内容
12.已知:△ABC的∠A的平分线和外接圆O相交于点D,BE是⊙O的切线,DF⊥BC,DG⊥BE,垂足分别为F、G.求证:DF=DG.分析 连接BD.由弦切角定理可知∠FBD=∠BAD,由同弧所对的圆周角相等可知:∠DBC=∠DAC,由角平分线的定义可知∠BAD=∠DAC,从而得到∠FBD=∠DBG,因为DF⊥BC,DG⊥BE由角平分线的性质可知FD=DG.
解答 解:如图所示:连接BD.
∵BE是圆O的切线,
∴∠FBD=∠BAD.
∵∠DBC=∠DAC,∠BAD=∠DAC,
∴∠FBD=∠DBG.
又∵DF⊥BC,DG⊥BE,
∴FD=DG.
点评 本题主要考查的是切线的性质,解答本题需要同学熟练掌握弦切角定理、圆周角定理以及角平分线的性质,证得∠FBD=∠DBG是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
20.下列计算中正确的是( )
| A. | (-3x3y3)2=3x6y6 | B. | a10•a2=a20 | ||
| C. | (-m2)5•(-m3)2=m16 | D. | (-$\frac{1}{2}$x2y4)3=-$\frac{1}{8}$x6y12 |
4.小敏到距家1500米的学校去上学,小敏出发10分钟后,小敏的爸爸立即去追小敏,且在距离学校60米的地方追上了她.已知爸爸比小敏的速度快100米/分,求小敏的速度.若设小敏的速度为x米/分,则根据题意所列方程正确的是( )
| A. | $\frac{1440}{x}=\frac{1440}{x+100}+10$ | B. | $\frac{1440}{x-100}-\frac{1440}{x}=10$ | ||
| C. | $\frac{1440}{x}=\frac{1440}{x-100}+10$ | D. | $\frac{1440}{x+100}-\frac{1440}{x}=10$ |
 如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.
如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE.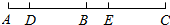 如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12.
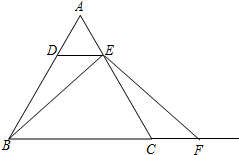
如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE=$\frac{1}{5}$AE,若DB=12. 如图,△DEF是由等腰△ABC经过平移得到的,其中AB=AC,且A与D、B与E、C与F分别是对应点,若∠B=50°,则∠D=80°.
如图,△DEF是由等腰△ABC经过平移得到的,其中AB=AC,且A与D、B与E、C与F分别是对应点,若∠B=50°,则∠D=80°.