题目内容
6．已知$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$，且x+y-z=2，求x、y、z的值．分析 根据等比性质，可用k表示x，y，z，根据解方程，可得k的值，可得答案．
解答 解：设$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$=k，得
x=2k，y=3k，z=4k．
将x=2k，y=3k，z=4k代入x+y-z=2，得
2k+3k-4k=2．
解得k=2．
x=2k=4，y=3k=6，z=4k=8．
点评 本题考查了比例的性质，利用等比性质得出k表示x，y，z是解题关键．
练习册系列答案
相关题目
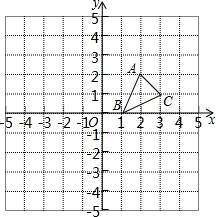如图，在建立了平面直角坐标系的正方形网格中，A（2，2），B（1，0），C（3，1）
如图，点C是反比例函数y=$\frac{k}{x}$图象的一点，点C的坐标为（4，-1）．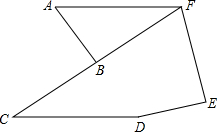
如图，已知AB=DE，BC=EF，CD=FA，∠ABC=86°，∠E=86°，求证：AF∥CD．