题目内容
1.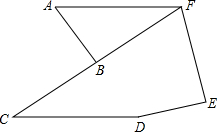 如图,已知AB=DE,BC=EF,CD=FA,∠ABC=86°,∠E=86°,求证:AF∥CD.
如图,已知AB=DE,BC=EF,CD=FA,∠ABC=86°,∠E=86°,求证:AF∥CD.
分析 连接AC、DF,利用“边角边”证明△ABC和△DEF全等,根据全等三角形对应边相等可得AC=FD,再利用“边边边”证明△ACF和△DFC全等,根据全等三角形对应角相等可得∠AFC=∠DCF,然后根据内错角相等,两直线平行证明即.
解答 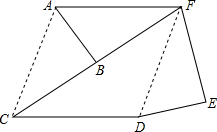 证明:如图,连接AC、DF,
证明:如图,连接AC、DF,
在△ABC和△DEF中,$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠E=86°}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴AC=FD,
在△ACF和△DFC中,$\left\{\begin{array}{l}{CD=FA}\\{AC=FD}\\{CF=FC}\end{array}\right.$,
∴△ACF≌△DFC(SSS),
∴∠AFC=∠DCF.
点评 本题考查了全等三角形的判定与性质,平行线的判定,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
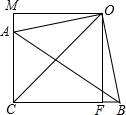 如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.
如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.