题目内容
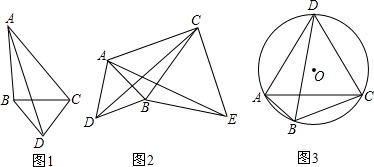
2. 一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)| A. | 26分 | B. | 25分 | C. | 24分 | D. | 23分 |
分析 根据∠AOD=45°,∠BOD=45°,AB∥x轴,△AOB为等腰直角三角形,OA=OB,根据AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{2}OA$,设行驶OA所用的时间为a分钟,则行驶OB所用的时间为a分钟,行驶AB所用的时间为$\sqrt{2}$a分钟,根据从O港出发,1小时后回到O港,得到a+a+$\sqrt{2}$a=60,求出a的值即可解答.
解答 解:如图,
∵∠AOD=45°,∠BOD=45°,
∴∠AOD=90°,
∵AB∥x轴,
∴∠BAO=∠AOC=45°,∠ABO=∠BOD=45°,
∴△AOB为等腰直角三角形,OA=OB,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{2}OA$,
设行驶OA所用的时间为a分钟,
则行驶OB所用的时间为a分钟,行驶AB所用的时间为$\sqrt{2}$a分钟,
∵从O港出发,1小时后回到O港,
∴a+a+$\sqrt{2}$a=60,
解得:a=$\frac{60}{2+\sqrt{2}}=30(2-\sqrt{2})$,
$\sqrt{2}$a=24,
故选:C.
点评 本题考查了等腰直角三角形,解决本题的关键是熟悉等腰直角三角形的性质.

练习册系列答案
相关题目
12. 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )| A. | 8 | B. | 3 | C. | 2 | D. | -3 |
13.已知a>b,则下列不等式关系中正确的是( )
| A. | ac>bc | B. | ac2>bc2 | C. | a-1>b+1 | D. | a+1>b-1 |
14. 如图,下列说法错误的是( )
如图,下列说法错误的是( )
 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | ∠1与∠2是同旁内角 | B. | ∠1与∠4是同旁内角 | ||
| C. | ∠5与∠3是内错角 | D. | ∠5与∠2是内错角 |
11.据了解,H7N9禽流感病毒的直径大约是0.00 000 008米,则0.00 000 008用科学记数法表示为( )
| A. | 0.8×107 | B. | 8×10-8 | C. | 8×10-7 | D. | 8×10-6 |
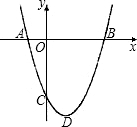 如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A,B两点,点A的坐标为(-1,0),与y轴交于点C(0,-2).
如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A,B两点,点A的坐标为(-1,0),与y轴交于点C(0,-2).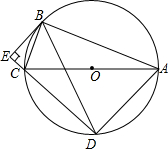 如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证: