题目内容
10.已知x、y为直角三角形的两边的长,满足(x-2)2+|(y-2)(y-3)|=0,则第三边的长为2$\sqrt{2}$或$\sqrt{13}$或$\sqrt{5}$.分析 先根据题意求出x、y的值,再分情况讨论,根据勾股定理即可求出第三边的长.
解答 解:∵(x-2)2+|(y-2)(y-3)|=0,
∴x-2=0,(y-2)(y-3)=0,
∴x=2,y=2,或y=3;
(1)当x=2,y=2时,x、y为直角边长,斜边长=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
(2)当x=2,y=3时,分两种情况:
①y为直角边长时,斜边长=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$;
②y为斜边时,第三边长=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$;
综上所述:第三边的长为2$\sqrt{2}$或$\sqrt{13}$或$\sqrt{5}$;
故答案为:2$\sqrt{2}$或$\sqrt{13}$或$\sqrt{5}$.
点评 本题考查了绝对值的性质、偶次方的性质、勾股定理的运用;熟练掌握绝对值和偶次方的性质,运用勾股定理求出第三边长是解决问题的关键;注意进行分类讨论,避免漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列计算结果错误的是( )
| A. | (-a3)2=a6 | B. | a2•a3=a6 | C. | ($\frac{1}{2}$)-1-22=-2 | D. | (cos60°-$\frac{1}{2}$)0=1 |
 如图,以⊙O上任意一点A为圆心,AO为半径画弧,与⊙O相交于B、C两点,点P为优弧BmC上任意一点,则∠P的度数是60°.
如图,以⊙O上任意一点A为圆心,AO为半径画弧,与⊙O相交于B、C两点,点P为优弧BmC上任意一点,则∠P的度数是60°.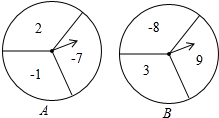 如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:
如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则: 一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)