题目内容
7.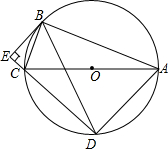 如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:(1)∠ECB=∠BAD;
(2)BE是⊙O的切线.
分析 (1)根据圆内接四边形的性质求得即可;
(2)连接OB,OD,证明△ABO≌△DBO,推出OB∥DE,继而判断BE⊥OB,可得出结论.
解答  (1)证明:∵四边形ABCD是圆内接四边形,
(1)证明:∵四边形ABCD是圆内接四边形,
∴∠ECB=∠BAD.
(2)证明:连结OB,OD,
在△ABO和△DBO中,
$\left\{\begin{array}{l}{AB=BD}\\{BO=BO}\\{OA=OD}\end{array}\right.$,
∴△ABO≌△DBO(SSS),
∴∠DBO=∠ABO,
∵∠ABO=∠OAB=∠BDC,
∴∠DBO=∠BDC,
∴OB∥ED,
∵BE⊥ED,
∴EB⊥BO,
∴BE是⊙O的切线.
点评 本题考查了圆内接四边形的性质、切线的判定、三角形全等的判定和性质、等腰三角形的性质、平行线的判定和性质,综合考查的知识点较多,熟练掌握定理的内容是解题的关键.

练习册系列答案
相关题目
2. 一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
 一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)
一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB∥x轴,则快艇驶完AB这段路程所用的时间为( )(取$\sqrt{2}$的值为1.4)| A. | 26分 | B. | 25分 | C. | 24分 | D. | 23分 |
12.下列说法错误的是( )
| A. | 若两角互余,则两角均为锐角 | B. | 若两角相等,则它们的补角也相等 | ||
| C. | 互为余角的补角相等 | D. | 两个钝角不能互补 |
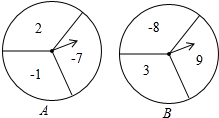 如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:
如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则: 如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.
如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.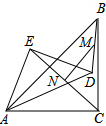 已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.
已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.