题目内容
17.如图①是一张可折叠的钢丝床示意图,这是展开后支撑起来放在地面上的情况.如果折叠起来,床头部分被折到了床面之下(这里的A,B,C,D各点都是活动的),其折叠过程可由图②的变换反映出来(1)活动床头的固定、折叠是根据三角形的稳定性和四边形的不稳定性而设计的;
(2)若图②中的四边形ACD的边AB=6,BC=14,当AD长为多少时,才能实现上述的折叠变化.
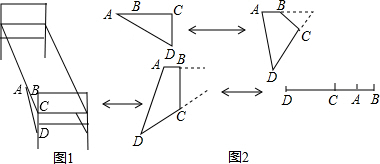
分析 (1)活动床头的固定、折叠是根据三角形的稳定性和四边形的不稳定性设计而成的;
(2)根据已知得出图形得出AC2+CD2=AD2,以及AB+AD=CD+BC,进而求出即可.
解答 解:(1)活动床头的固定、折叠是根据三角形的稳定性和四边形的不稳定性而设计的;
(2)由图2的第一个图形得:AC2+CD2=AD2,
即(6+14)2+CD2=AD2①,
由图2的第三四个图形得:AB+AD=CD+BC
即6+AD=CD+14②,
联立①②,解得AD=29
所以当AD长为29时,才能实现上述的折叠变化.
点评 此题主要考查了翻折变换的性质以及勾股定理的运用,得出正确的等量关系是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
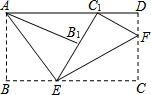
6.如图,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则Sn=( )(用含n的式子表示)

| A. | $\frac{\sqrt{3}n}{n+1}$ | B. | $\frac{\sqrt{2}n}{2n+2}$ | C. | $\frac{n}{2n+2}$ | D. | $\frac{\sqrt{3}n}{{n}^{2}+2n}$ |

 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AD=3,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处,则DC的长为$\sqrt{3}$.
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AD=3,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处,则DC的长为$\sqrt{3}$.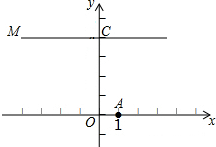 如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD.
如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD. 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数.