Question

12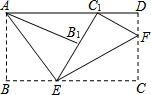．将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，AD=3，折叠后，点C落在AD边上的C₁处，并且点B落在EC₁边上的B₁处，则DC的长为$\sqrt{3}$．

Answer 1

分析 设AB=x，由三角函数易得BE，AE长，根据翻折和对边平行可得△AEC₁和△CEC₁为等边三角形，那么就得到EC长，相加得出BC，进一步求得AB即可．

解答 解：连接CC₁，设AB=x，
∵Rt△ABE中，∠BAE=30°，
∴BE=AB×tan30°=$\frac{\sqrt{3}}{3}$x，AE=$\frac{2\sqrt{3}}{3}$x．∠AEB₁=∠AEB=60°，
∵AD∥BC，
∴∠C₁AE=∠AEB=60°，
∴△AEC₁为等边三角形，
∴△CC₁E也为等边三角形，
∴EC=EC₁=AE=$\frac{2\sqrt{3}}{3}$x，
∴AD=BC=BE+EC=3，
即$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$x=3，
x=$\sqrt{3}$，
∴DC=AB=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题通过折叠变换考查学生的逻辑思维能力，注意使用翻折前后得到的对应边相等，对应角相等这个知识点及相应的三角函数等知识．