题目内容

19．如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，求BC的长．

分析 首先根据三角形外角的性质可得∠B=∠BAD，根据等角对等边可得BD=AD=$\sqrt{5}$，然后利用勾股定理计算出CD长，进而可得BC长．

解答 解：∵∠B+∠DAB=∠ADC，∠ADC=2∠B，
∴∠B=∠BAD，
∴BD=AD=$\sqrt{5}$，
∵∠C=90°，
∴CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{5-4}$=1，
∴BC=$\sqrt{5}$+1．

点评 此题主要考查了勾股定理，以及三角形外角的性质，关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．

练习册系列答案
相关题目
14．如图，小明在大楼30米高即（PH=30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚处的俯角为60°．已知该山坡的坡度i（即tan∠ABC）为1：$\sqrt{3}$，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC，则A到BC的距离为10$\sqrt{3}$米．
10．有一块直角三角形的绿地，量得两直角边BC、AC分别为6m，8m，现在要将绿地扩充成等腰三角形，且扩充部分是以AC边为直角边的直角三角形，求扩充后等腰三角形绿地的面积．（图2，图3备用）
7．某数的平方根为2a+3与a-15，这个数是（　　）
A．121B．11C．±11D．4
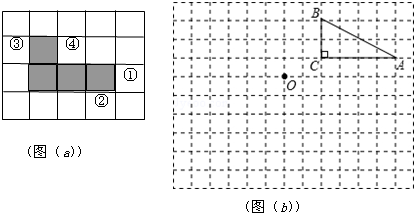
14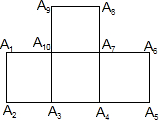．如图，在四个正方形拼接成的图形中，以这十个点中任意三点为顶点，共能组成（　　）个等腰直角三角形．
A．18B．22C．24D．26
4．若$\sqrt{48n}$是正整数，则最小的整数n是3．
11．在△ABC中，AB=AC，∠ABC=∠ACB，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接BE．
（1）如图1，当点D在线段BC上，
①如果∠BAC=90°，△ABD与△ACE全等吗？并求∠BCE度数；
②如果∠BAC=100°，直接写出∠BCE的度数．
（2）设∠BAC=α，∠BCE=β．
①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；
②当点D在直线BC上移动，则α，β之间有怎样的数量关系？请在备用图上画出图形，直接写出你的结论．
8．（1）如图（a）在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号是②．
（2）如图（b），在边长为1个单位长度的小正方形组成的网格中，点A、B、C都是格点．
①将△ABC向左平移6个单位长度得到得到△A1B1C1，并画出△A1B1C1；
②将△A1B1C1绕点O按逆时针方向旋转90°得到△A2B2C2，请画出△A2B2C2；
③将△A1B1C1绕点O旋转180°得到△A3B3C3，请画出△A3B3C3．
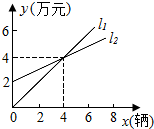9．如图，l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系；l2表示该电动车厂一天的销售成本与销售量的关系．
（1）写出销售收入与销售量之间的函数关系式？
（2）写出销售成本与销售之间的函数关系式？
（3）当一天的销售量为多少辆时，销售收入等于销售成本？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网