题目内容
13.探究题:在下列图形中,已知AB∥CD,请你解答以下问题:(1)图①中,∠A+∠C=180度,说明理由.
(2)在A、C之间加一个折点O1时,如图②,则∠A+∠O1+∠C=360度.
(3)在A、C之间加二个折点O1、O2时,如图③,则∠A+∠O1+∠O2+∠C=540度.…
(4)在A、C之间加n个折点O1、O2、…O3时,如图m,你又有什么发现?请你用含n的代数式写出你发现的结论.

分析 (1)根据平行线的性质可直接得到结论;
(2)过点O1作AB的平行线,利用平行线的性质,计算出∠A+∠O1+∠C度数;
(3)过点O1作AB的平行线,利用平行线的性质,计算出∠A+∠O1+∠O2+∠C度数;
(4)通过前三个,找出规律.利用规律得到有n个折点的结论.
解答  解:(1)故答案为:180;理由:
解:(1)故答案为:180;理由:
如右图所示:∵AB∥CD,
∴∠A+∠C=180°.(两直线平行,同旁内角互补)
(2)过O1作O1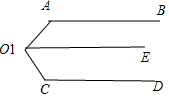 E∥AB
E∥AB
∴∠A+∠AO1E=180°,
∵AB∥CD
∴O1E∥CD,
∴∠EO1C+∠C=180°.
∴∠A+∠AO1E+∠EO1C+∠C=360°,
即∠A+∠AO1C+∠C=360°;
故答案为:360
(3)过O1、O2作O1E∥AB,O2F∥AB
∵AB∥CD
∴AB∥O1E∥O2F∥CD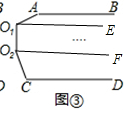 ∴∠A+∠AO1E=180°,
∴∠A+∠AO1E=180°,
∠EO1O2+∠O1O2F=180°
∠FO2C+∠C=180°
∴∠A+∠AO1E+∠EO1O2+∠O1O2F+∠FO2C+∠C=180°×3
即∠A+∠AO1O2+∠O1O2C+∠C=540°;
故答案为:540
(4)由当平行线AB与CD间没有点的时候,∠A+∠C=180°,
当A、C之间加一个折点O1时,∠A+∠O1+∠C=2×180°;
当A、C之间加二个折点O1、O2时,则∠A+∠O1+∠O2+∠C=3×180°;
当A、C之间加三个折点O1、O2、O3时,
则∠A+∠O1+∠O2+∠O3+∠C=4×180°;
在A、C之间加n个折点O1、O2、…On时,
则∠A+∠O1+∠O2+∠O3+…∠On+∠C=(n+1)×180°.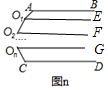
点评 本题考查了平行线的性质.过折点作平行线是解决问题的关键.另也可以作如图的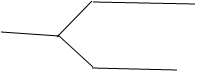 辅助线,利用平行线的性质和周角.
辅助线,利用平行线的性质和周角.

练习册系列答案
相关题目
16.下列各数是无理数的为( )
| A. | -9 | B. | $\frac{π}{3}$ | C. | 4.121121112 | D. | $\frac{22}{7}$ |
17.在实数-$\frac{2}{7}$,0,π,$\sqrt{5}$,1.41中,无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.下列数据中最小的是( )
| A. | 11011001(二进制数) | B. | 75(十进制数) | ||
| C. | 72(八进制数) | D. | 57(十六制数) |
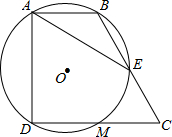 如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
 如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$.
如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$.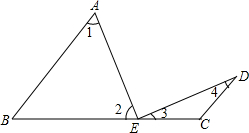 已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.
已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.