Question

1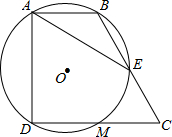．如图，已知直角梯形ABCD中，∠BAD=∠CDA=90°，CD=2AB，过A、B、D三点的⊙O分别交BC、CD于E、M．
（1）求证：DM=CM；
（2）若CE=2，CM=$\sqrt{6}$，求AE的长．

Answer 1

分析 （1）连接BD，BM，AM，EM，DE，由90度角所对的弦为直径，得到BD为圆的直径，再利用直径所对的圆周角为直角，得到∠BMD为直角，利用三个角为直角的四边形为矩形得到ABMD为矩形，利用矩形的对边相等得到AB=DM，而DC=2AB，等量代换得到CD=2DM，可得出M为DC的中点，即DM=CM；
（2）由BM⊥CD，DM=CM，得到BD=BC，根据勾股定理得到DE=$\sqrt{D{C}^{2}-E{C}^{2}}$=2$\sqrt{5}$，设BE=x，BD=BC=BE+EC=x+2，根据勾股定理列方程得到BD=6，在直角三角形AEM中，由AM与ME的长，利用勾股定理求出AE的长．

解答 解：（1）连接BD，BM，AM，EM，DE，
∵∠BAD=90°，
∴BD为圆的直径，
∴∠BMD=90°，
∴∠BAD=∠CDA=∠BMD=90°，
∴四边形ABMD矩形，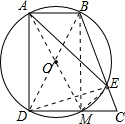
∴AB=DM，
又∵CD=2AB，
∴CD=2DM，即DM=MC；
（2）∵BM⊥CD，DM=CM，
∴BD=BC，
∵AM=BD，
∴AM=BC，
∵BD是直径，
∴∠BED=90°，即∠DEC=90°，
又EC=2，DC=2CM=2$\sqrt{6}$，
根据勾股定理得：DE=$\sqrt{D{C}^{2}-E{C}^{2}}$=2$\sqrt{5}$，
设BE=x，BD=BC=BE+EC=x+2，
在Rt△BDE中，根据勾股定理得：BE²+DE²=BD²，即x²+20=（x+2）²，
解得：x=4，
∴BD=6，在Rt△AEM中，AM=6，EM=$\sqrt{6}$，
根据勾股定理得：AE=$\sqrt{A{M}^{2}-E{M}^{2}}$=$\sqrt{30}$．

点评 本题考查了圆周角定理，圆心角、弦及弧之间的关系，勾股定理，矩形的判定与性质，利用了方程的思想，熟练掌握性质及定理是解本题的关键．