题目内容
2．若顺次连接四边形ABCD的四边中点得到的四边形为菱形，则四边形ABCD需满足条件对角线相等．分析 根据中点四边形的性质即可求出答案．
解答 解：由于顺次连接四边形ABCD的四边中点得到的四边形必为平行四边形，
∴该中点四边形为菱形时，其四边形ABCD的对角线必定相等，
故答案为：对角线相等．
点评 本题考查中点四边形，解题的关键是正确理解中点四边形的性质，本题属于基础题型．
练习册系列答案
名校课堂系列答案
相关题目
1．下列各组式子中，是同类项的是（ ）
| A． | $\frac{1}{5}$mn与5m2n | B． | 5ab与5abc | C． | 2x2y与2a2b | D． | 2x3y2与$\frac{1}{2}$y2x3 |
19．
如图，正方形OABC在平面直角坐标系中，点A的坐标为（2，0），将正方形OABC绕点O顺时针旋转45°，得到正方形OA′B′C′，则点C′的坐标为（ ）
如图，正方形OABC在平面直角坐标系中，点A的坐标为（2，0），将正方形OABC绕点O顺时针旋转45°，得到正方形OA′B′C′，则点C′的坐标为（ ）| A． | （$\sqrt{2}$，$\sqrt{2}$） | B． | （-$\sqrt{2}$，$\sqrt{2}$） | C． | （$\sqrt{2}$，$-\sqrt{2}$） | D． | （2$\sqrt{2}$，2$\sqrt{2}$） |
如图所示，当剪刀口∠AOB增大20°时，∠COD增大20° 度，其根据是对顶角相等．
已知：如图，在?ABCD中，AB=2cm，AD=5cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=3cm．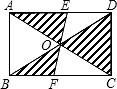
如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=4cm，BC=6cm，则图中阴影部分的面积为12cm2．